题目内容
【题目】已知函数
，(
)．
（1）若函数
与
的图象在
上有两个不同的交点，求实数
的取值范围；
（2）若在
上不等式
恒成立，求实数的取值范围；
（3）证明：对于
时，任意
，不等式
恒成立．
【答案】（1）
；（2）
；（3）见解析.
【解析】【试题分析】（1）依据题设将问题进行转化，再运用导数知识求解；（2）先将不等式进行等价转化，再构造函数借助导数工具分析求解；（3）先构造函数，再依据题设与问题（2）的结论进行分析推证。
（1）设函数
，
①
时，
为单调减函数，不成立
②
时，
，
；
，
所以函数有唯一的极小值，需要
，
又因为
，
，
所以在
有两个零点，
，
有两个交点，
所以
（2）设函数
，且
①当时，有
，不成立，
②当时，（i）时，
，当
时，
所以
在上是单调增函数，所以
（ii）
时，设
，
所以存在
，使得
时
，∴
，
不成立
综上所述
（3）不等式变形为
设函数
，由第（2）问可知当
时函数
为单调函数，所以原不等式成立．
【题目】随着移动互联网时代的到来，手机的使用非常普遍，“低头族”随处可见。某校为了解家长和教师对学生带手机进校园的态度，随机调查了100位家长和教师，得到情况如下表：
教师 | 家长 | |
反对 | 40 | 20 |
支持 | 20 | 20 |
（1）是否有95%以上的把握认为“带手机进校园与身份有关”，并说明理由；
（2）把以上频率当概率，随机抽取3位教师，记其中反对学生带手机进校园的人数为X，求随机变量X的分布列和数学期望．
附：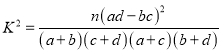 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
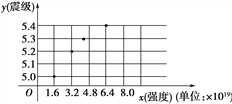
【题目】某地区发生里氏8.0级特大地震．地震专家对发生的余震进行了监测，记录的部分数据如下表：
强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
注：地震强度是指地震时释放的能量．
地震强度(x)和震级(y)的模拟函数关系可以选用y＝alg x＋b(其中a，b为常数)．利用散点图(如图)可知a的值等于________．(取lg 2＝0.3进行计算)
