题目内容
(本小题满分12分)(注意:在试题卷上作答无效)
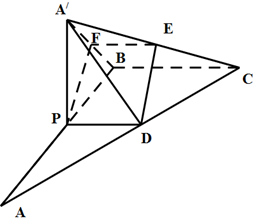
函数 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若函数 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围;
(Ⅲ)是否存在点P,使得过点P的直线若能与曲线 围成两个封闭图形,则这两个封闭图形的面积相等?若存在,求出P点的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积相等?若存在,求出P点的坐标;若不存在,说明理由.
函数
 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
.(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)若函数
 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围;(Ⅲ)是否存在点P,使得过点P的直线若能与曲线
 围成两个封闭图形,则这两个封闭图形的面积相等?若存在,求出P点的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积相等?若存在,求出P点的坐标;若不存在,说明理由.解:(Ⅰ)由题意得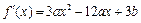 ,
,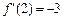 且
且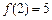 ,
,
∴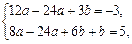 即
即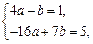 解得
解得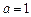 ,
,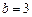 ,
,
∴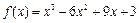 .······················· 4分
.······················· 4分
(Ⅱ)由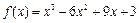 ,可得
,可得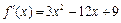 ,
,
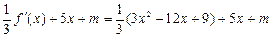
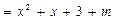 ,
,
则由题意可得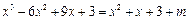 有三个不相等的实根,
有三个不相等的实根,
即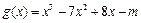 的图象与
的图象与 轴有三个不同的交点,
轴有三个不同的交点,
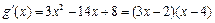 ,则
,则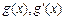 的变化情况如下表.
的变化情况如下表.
则函数 的极大值为
的极大值为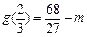 ,极小值为
,极小值为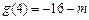 .······ 6分
.······ 6分
 的图象与
的图象与 的图象有三个不同交点,则有:
的图象有三个不同交点,则有:
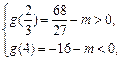 解得
解得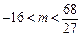 .·················· 8分
.·················· 8分
(Ⅲ)存在点P满足条件.························· 9分
∵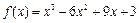 ,∴
,∴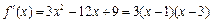 ,由
,由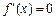 ,得
,得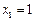 ,
,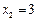 .当
.当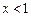 时,
时,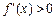 ;当
;当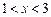 时,
时,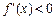 ;当
;当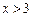 时,
时,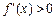 .可知极值点为
.可知极值点为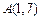 ,
,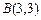 ,线段AB中点
,线段AB中点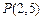 在曲线
在曲线 上,且该曲线关于点
上,且该曲线关于点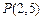 成中心对称.证明如下:∵
成中心对称.证明如下:∵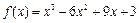 ,∴
,∴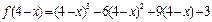
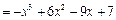 ,∴
,∴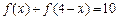 .
.
上式表明,若点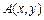 为曲线
为曲线 上任一点,其关于
上任一点,其关于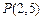 的对称点
的对称点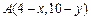 也在曲线
也在曲线 上,曲线
上,曲线 关于点
关于点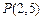 对称.故存在点
对称.故存在点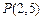 ,使得过该点的直线若能与曲线
,使得过该点的直线若能与曲线 围成两个封闭图形,这两个封闭图形的面积相等.………………12分
围成两个封闭图形,这两个封闭图形的面积相等.………………12分
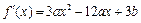 ,
,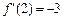 且
且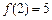 ,
,∴
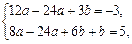 即
即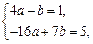 解得
解得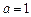 ,
,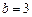 ,
,∴
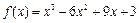 .······················· 4分
.······················· 4分(Ⅱ)由
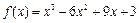 ,可得
,可得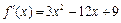 ,
,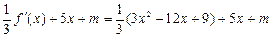
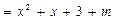 ,
,则由题意可得
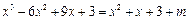 有三个不相等的实根,
有三个不相等的实根,即
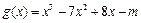 的图象与
的图象与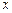 轴有三个不同的交点,
轴有三个不同的交点,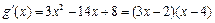 ,则
,则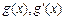 的变化情况如下表.
的变化情况如下表. | 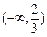 | 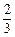 | 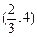 | 4 | 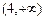 |
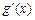 | + | 0 | - | 0 | + |
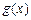 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
 的极大值为
的极大值为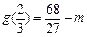 ,极小值为
,极小值为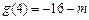 .······ 6分
.······ 6分 的图象与
的图象与 的图象有三个不同交点,则有:
的图象有三个不同交点,则有: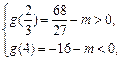 解得
解得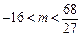 .·················· 8分
.·················· 8分(Ⅲ)存在点P满足条件.························· 9分
∵
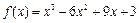 ,∴
,∴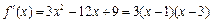 ,由
,由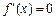 ,得
,得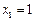 ,
,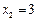 .当
.当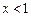 时,
时,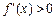 ;当
;当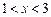 时,
时,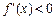 ;当
;当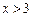 时,
时,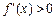 .可知极值点为
.可知极值点为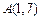 ,
,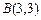 ,线段AB中点
,线段AB中点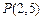 在曲线
在曲线 上,且该曲线关于点
上,且该曲线关于点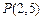 成中心对称.证明如下:∵
成中心对称.证明如下:∵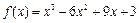 ,∴
,∴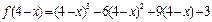
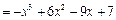 ,∴
,∴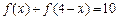 .
.上式表明,若点
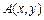 为曲线
为曲线 上任一点,其关于
上任一点,其关于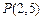 的对称点
的对称点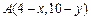 也在曲线
也在曲线 上,曲线
上,曲线 关于点
关于点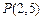 对称.故存在点
对称.故存在点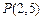 ,使得过该点的直线若能与曲线
,使得过该点的直线若能与曲线 围成两个封闭图形,这两个封闭图形的面积相等.………………12分
围成两个封闭图形,这两个封闭图形的面积相等.………………12分略

练习册系列答案
相关题目
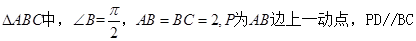 交AC于 点D,现将
交AC于 点D,现将
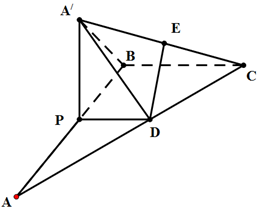
 的体积最大时,求PA的长;
的体积最大时,求PA的长;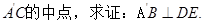
 在
在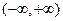 上是增函数,求b的取值范围;
上是增函数,求b的取值范围;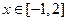 时,
时,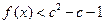 恒成立,求c的取值范围.
恒成立,求c的取值范围.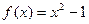 与函数
与函数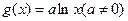 .
.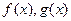 的图象
的图象 在点
在点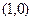 处有公共的切线,求实数
处有公共的切线,求实数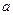 的值;
的值;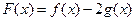 ,求函数
,求函数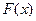 的极值.
的极值. 单调递增区间为
单调递增区间为 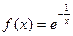 ,则
,则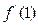 = ___________.
= ___________.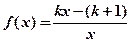
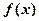 是
是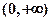 上的增函数,求
上的增函数,求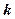 的取值范围;
的取值范围;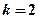 时,不等式
时,不等式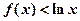 对任意
对任意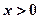 恒成立;
恒成立;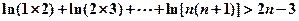
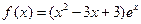
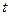 的取值范围,使得函数
的取值范围,使得函数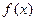 在
在 上为单调函数;
上为单调函数; 时,判断
时,判断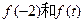 的大小,并说明理由;
的大小,并说明理由;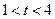 时,关于
时,关于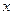 的方程
的方程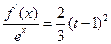 在区间
在区间