题目内容
【题目】如图，椭圆C： 
=1（a＞b＞0）的离心率为 
，其左焦点到点P（2，1）的距离为 
，不过原点O的直线l与C相交于A，B两点，且线段AB被直线OP平分． 
（1）求椭圆C的方程；
（2）求△APB面积取最大值时直线l的方程．
【答案】
（1）解：由题意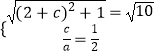 
，解得： 
．
∴所求椭圆C的方程为： 
．
（2）解：设A（x1，y1），B（x2，y2），线段AB的中点为M
当AB⊥x轴时，直线AB的方程为x=0，与不过原点的条件不符，故设AB的方程为y=kx+m（m≠0）
由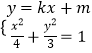 
，消元可得（3+4k2）x2+8kmx+4m2﹣12=0①
∴ 
， 
∴线段AB的中点M 
∵M在直线OP上，∴ 
∴k=﹣ 
故①变为3x2﹣3mx+m2﹣3=0，又直线与椭圆相交，
∴△＞0，x1+x2=m， 
∴|AB|= 
P到直线AB的距离d= 
∴△APB面积S= 
（m∈（﹣2 
，0） 
令u（m）=（12﹣m2）（m﹣4）2，则 
∴m=1﹣ 
，u（m）取到最大值
∴m=1﹣ 时，S取到最大值
综上，所求直线的方程为： 
【解析】（1）由题意，根据离心率为 
，其左焦点到点P（2，1）的距离为 
，建立方程，即可求得椭圆C的方程；（2）设A（x1 ， y1），B（x2 ， y2），线段AB的中点为M，当AB⊥x轴时，直线AB的方程为x=0，与不过原点的条件不符，故设AB的方程为y=kx+m（m≠0）由 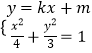，消元再利用韦达定理求得线段AB的中点M，根据M在直线OP上，可求|AB|，P到直线AB的距离，即可求得△APB面积，从而问题得解．
【考点精析】关于本题考查的椭圆的标准方程，需要了解椭圆标准方程焦点在x轴：
，焦点在y轴：
才能得出正确答案．
新非凡教辅冲刺100分系列答案【题目】为了了解我市特色学校的发展状况，某调查机构得到如下统计数据：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（Ⅰ）根据上表数据，计算
与
的相关系数
，并说明与的线性相关性强弱（已知：
，则认为与线性相关性很强；
，则认为与线性相关性一般；
，则认为与线性相关性较弱）；
（Ⅱ）求关于的线性回归方程，并预测我市2019年特色学校的个数（精确到个）．
参考公式：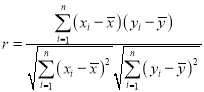 
，
，
，
，
，
．
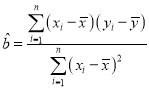【题目】某商场经营一批进价是30元/件的商品，在市场试销中发现，此商品销售价
元与日销售量
件之间有如下关系：
x | 45 | 50 |
y | 27 | 12 |
（1）确定与的一个一次函数关系式
；
（2）若日销售利润为P元，根据（Ｉ）中关系写出P关于的函数关系，并指出当销售单价为多少元时，才能获得最大的日销售利润？
【题目】对某校高三年级学生参加社区服务次数进行统计，随机抽取
名学生作为样本，得到这名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：
分组 | 频数 | 频率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合计 |
| 1 |
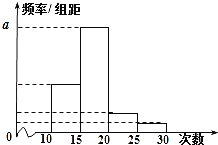
（1）求出表中，
及图中
的值；
（2）若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间
内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间
内的概率．
