题目内容
某人摆一个摊位卖小商品,一周内出摊天数x与盈利y(百元),之间的一组数据关系见表:
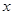 | 2 | 3 | 4 | 5 | 6 |
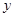 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
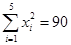 ,
,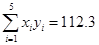 ,
,(1)在下面坐标系中画出散点图;

(2)计算
 ,
,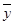 ,并求出线性回归方程;
,并求出线性回归方程;(3)在第(2)问条件下,估计该摊主每周7天要是天天出摊,盈利为多少?
(1)散点图详见解析;(2)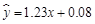 ;(3)8.69(百元).
;(3)8.69(百元).
解析试题分析:(1)将表格中数据转化为相应点的坐标: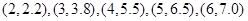 将其花在坐标系上,即可得到散点图;(2)根据线性回归的相关公式:
将其花在坐标系上,即可得到散点图;(2)根据线性回归的相关公式: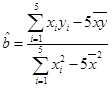 ,
,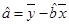 ,而根据表格中数据,易得
,而根据表格中数据,易得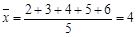 ,
,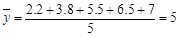 ,从而求得线性回归方程为
,从而求得线性回归方程为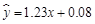 ;(3)利用(2)中所求得的线性回归方程可知:当
;(3)利用(2)中所求得的线性回归方程可知:当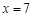 时,
时,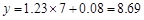 .
.
因此该摊主每周7天要是天天出摊,估计盈利为8.69(百元).
(1)由表格中相关数据,易得散点图为: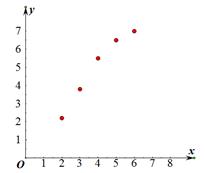 2分;
2分;
(2)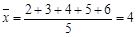 ,
,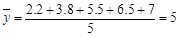 . 4分
. 4分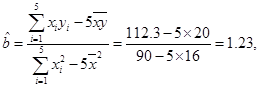 6分
6分
∴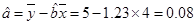 7分
7分
故所求回归直线方程为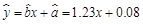 . 8分;
. 8分;
(3)当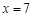 时,
时,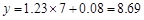 .
.
∴该摊主每周7天要是天天出摊,估计盈利为8.69(百元). 10分.
考点:线性回归分析的运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16.
| | 第一批次 | 第二批次 | 第三批次 |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
(1)求x的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
某普通高中共有教师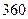 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 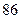 |  |  |
| 男教师 | 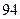 | 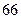 |  |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是
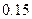 、
、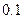 .
.(1)求
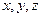 的值;
的值;(2)为了调查研修效果,现从三个批次中按
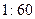 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?(3)若从(2)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |  组 组 | 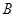 组 组 |  组 组 |
| 疫苗有效 | 673 | 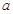 | 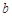 |
| 疫苗无效 | 77 | 90 | 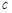 |
已知在全体样本中随机抽取1个,抽到
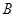 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33.(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在
 组抽取样本多少个?
组抽取样本多少个?(2)已知
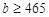 ,
,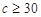 ,求通过测试的概率.
,求通过测试的概率. 
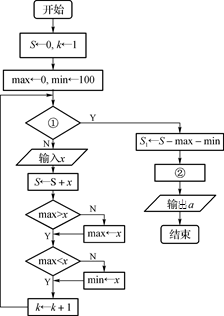

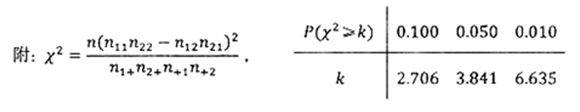


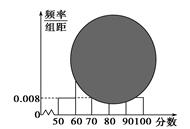
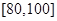 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在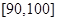 之间的概率;
之间的概率;