题目内容
已知在直角坐标系xOy中,曲线C的参数方程为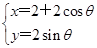 (θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin 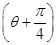 =2
=2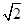 .
.
(1)求曲线C在极坐标系中的方程;
(2)求直线l被曲线C截得的弦长.
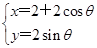 (θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin 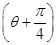 =2
=2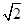 .
.(1)求曲线C在极坐标系中的方程;
(2)求直线l被曲线C截得的弦长.
(1)ρ=4cos θ.(2)2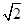
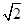
(1)由已知得,曲线C的普通方程为(x-2)2+y2=4,
即x2+y2-4x=0,化为极坐标方程是ρ=4cos θ.
(2)由题意知,直线l的直角坐标方程为x+y-4=0,
由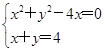 得直线l与曲线C的交点坐标为(2,2),(4,0),所以所求弦长为2
得直线l与曲线C的交点坐标为(2,2),(4,0),所以所求弦长为2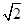
即x2+y2-4x=0,化为极坐标方程是ρ=4cos θ.
(2)由题意知,直线l的直角坐标方程为x+y-4=0,
由
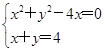 得直线l与曲线C的交点坐标为(2,2),(4,0),所以所求弦长为2
得直线l与曲线C的交点坐标为(2,2),(4,0),所以所求弦长为2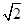

练习册系列答案
相关题目
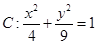 ,直线
,直线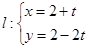 (
(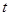 为参数)
为参数)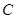 的参数方程,直线
的参数方程,直线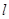 的普通方程;
的普通方程;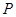 作与
作与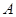 ,求
,求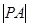 的最大值与最小值.
的最大值与最小值.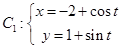 (
(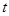 为参数),
为参数),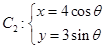 (
(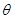 为参数).
为参数).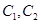 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;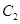 的左顶点且倾斜角为
的左顶点且倾斜角为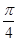 的直线
的直线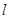 交曲线
交曲线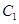 于
于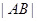 两点,求
两点,求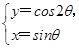 化为普通方程,并说明它表示的图形.
化为普通方程,并说明它表示的图形.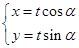 (
(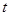 为参数)被圆
为参数)被圆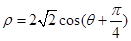 截得的弦长为最大,则此直线的倾斜角为 ;
截得的弦长为最大,则此直线的倾斜角为 ;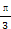 )且和极轴成
)且和极轴成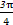 角的直线.
角的直线.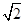 倍.
倍.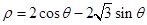 ,则圆的圆心的极坐标是
,则圆的圆心的极坐标是 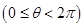 .
.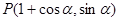 ,参数
,参数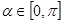
 ,点Q在曲线C:
,点Q在曲线C: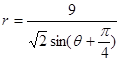 上.
上.