题目内容
将参数方程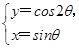
化为普通方程，并说明它表示的图形．
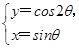化为普通方程，并说明它表示的图形．y＝1－2x2，抛物线的一部分．
由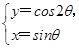可得
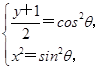即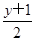
＋x2＝1，化简得y＝1－2x2.又－1≤x2＝sin2θ≤1，则－1≤x≤1，则普通方程为y＝1－2x2，在
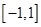时此函数图象为抛物线的一部分．
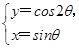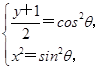可得即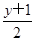＋x2＝1，化简得y＝1－2x2.又－1≤x2＝sin2θ≤1，则－1≤x≤1，则普通方程为y＝1－2x2，在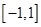时此函数图象为抛物线的一部分．
练习册系列答案
中考解读考点精练系列答案
相关题目
（
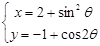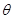为参数）化为普通方程是 .
为参数,则圆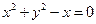
的参数方程为 .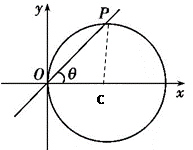
(t为参数)过椭圆C：
(φ为参数)的右顶点，求常数a的值．
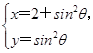(θ为参数)化为普通方程．
与曲线
在它们的公共点
处具有具有公共切线，则
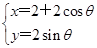(θ为参数)，在极坐标系(与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴)中，直线l的方程为ρsin 
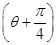＝2
.
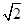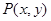是曲线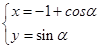
上任意一点，则
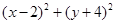的最大值是 （ ）