Question

【题目】已知双曲线的两个焦点为，，并且经过点.

（1）求双曲线的方程；

（2）过点的直线与双曲线有且仅有一个公共点，求直线的方程.

Answer 1

【答案】（1）；（2）或

【解析】

（1）利用，以及列方程组，解方程组求得，由此求得双曲线的方程.

（2）当直线斜率不存在时，直线与双曲线没有交点.当直线斜率存在时，设出直线的方程，联立直线的方程和双曲线的方程，消去得到，根据二次项系数和判别式进行分类讨论，由此求得直线的方程.

（1）由已知可设双曲线的方程为，

则，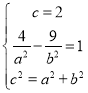

解得，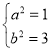

所以双曲线的方程为.

（2）当直线斜率不存在时，显然不合题意

所以可设直线方程为，

联立，得，

①当，即或，方程只有一解，直线与双曲线有且仅有一个公共点，此时，直线方程为，

②当，即，要使直线与双曲线有且仅有一个公共点，

则，解得，

此时，直线方程为，

综上所述，直线的方程为或.