题目内容
已知抛物线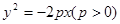 的焦点F恰好是椭圆
的焦点F恰好是椭圆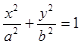 的左焦点,且两曲线的公共点的连线过F,则该椭圆的离心率为
的左焦点,且两曲线的公共点的连线过F,则该椭圆的离心率为
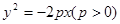 的焦点F恰好是椭圆
的焦点F恰好是椭圆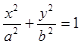 的左焦点,且两曲线的公共点的连线过F,则该椭圆的离心率为
的左焦点,且两曲线的公共点的连线过F,则该椭圆的离心率为 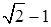
分析:由题意知,两曲线的公共点的连线和x轴垂直,c=" p/2" ,由椭圆的离心率的定义得e,从而解方程求得离心率的值。
解答:
题意知 F(- p/2,0),再由两曲线都关于x轴对称可知,两曲线的公共点的连线和x轴垂直,故c= p/2。
由椭圆的离心率的定义得e= p/(-c+ a2/c)=2c2/(a2-c2)=2e2/(1-e2),
∴2e=1-e2,又 0<e<1,∴e=
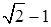
点评:本题考查椭圆、抛物线的标准方程,以及椭圆、抛物线的简单性质的应用。

练习册系列答案
相关题目
 2,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为
2,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为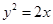 ,过动点
,过动点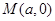 且斜率为1的直线
且斜率为1的直线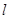 与抛物线交于不同两点A、B,|AB|
与抛物线交于不同两点A、B,|AB|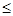 2.
2.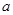 的取值范围;
的取值范围;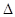 NAB面积的最大值.
NAB面积的最大值.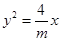 的焦点与椭圆
的焦点与椭圆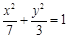 的左焦点重合,则
的左焦点重合,则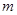 的值为( )
的值为( )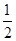
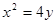 的焦点坐标是
的焦点坐标是 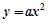 的准线方程是
的准线方程是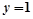 ,则
,则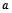 的值为( )
的值为( )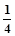
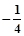
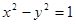 的中心,焦点是双曲线的右顶点.
的中心,焦点是双曲线的右顶点.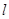 过点
过点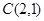 交抛物线于
交抛物线于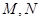 两点,是否存在直线
两点,是否存在直线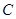 恰为弦
恰为弦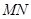 的中点?若存在,求出直线
的中点?若存在,求出直线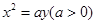 的焦点恰好为双曲线
的焦点恰好为双曲线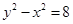 的焦点,则a=
的焦点,则a=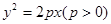 的焦点为
的焦点为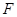 ,过点
,过点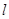 与抛物线交于
与抛物线交于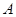 、
、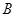 两点,抛物线的准线与
两点,抛物线的准线与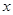 轴交于点
轴交于点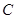 .
.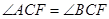 ;
;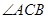 的最大值,并求
的最大值,并求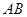 的长.
的长.