题目内容
已知抛物线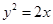 ,过动点
,过动点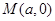 且斜率为1的直线
且斜率为1的直线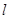 与抛物线交于不同两点A、B,|AB|
与抛物线交于不同两点A、B,|AB|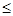 2.
2.
(1)求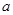 的取值范围;
的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求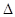 NAB面积的最大值.
NAB面积的最大值.
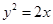 ,过动点
,过动点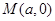 且斜率为1的直线
且斜率为1的直线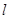 与抛物线交于不同两点A、B,|AB|
与抛物线交于不同两点A、B,|AB|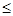 2.
2.(1)求
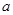 的取值范围;
的取值范围;(2)若线段AB的垂直平分线交x轴于点N,求
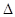 NAB面积的最大值.
NAB面积的最大值.(1)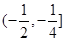 ;(2)
;(2)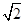 .
.
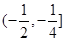 ;(2)
;(2)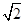 .
.(1)直线l的方程为:y=x-a,然后与抛物线方程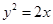 消x,借助弦长公式
消x,借助弦长公式
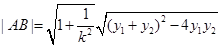 求出|AB|,再根据|AB|
求出|AB|,再根据|AB|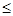 2,解关于a的不等式即可求解.
2,解关于a的不等式即可求解.
(2)再第(1)问的基础上求出弦AB中点Q的坐标,然后求出AB的垂直平分线方程,进而求出点N的坐标,
则|NQ|的长度就是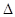 NAB的高,然后建立
NAB的高,然后建立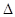 NAB面积与a的函数关系式,根据函数求最值的方法求解.
NAB面积与a的函数关系式,根据函数求最值的方法求解.
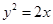 消x,借助弦长公式
消x,借助弦长公式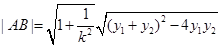 求出|AB|,再根据|AB|
求出|AB|,再根据|AB|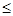 2,解关于a的不等式即可求解.
2,解关于a的不等式即可求解.(2)再第(1)问的基础上求出弦AB中点Q的坐标,然后求出AB的垂直平分线方程,进而求出点N的坐标,
则|NQ|的长度就是
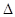 NAB的高,然后建立
NAB的高,然后建立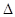 NAB面积与a的函数关系式,根据函数求最值的方法求解.
NAB面积与a的函数关系式,根据函数求最值的方法求解.
练习册系列答案
相关题目
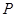 是抛物线
是抛物线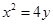 上的一个动点,则点
上的一个动点,则点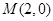 的距离与点
的距离与点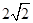
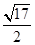
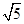
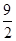
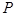 是曲线
是曲线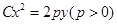 上的动点,点
上的动点,点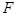 的距离之和的最小值为
的距离之和的最小值为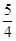 .
.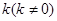 的直线交
的直线交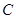 于点
于点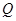 ,交
,交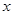 轴于点
轴于点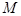 ,过点
,过点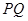 垂直的直线与
垂直的直线与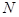 ,问是否存在实数
,问是否存在实数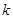 ,使得直线
,使得直线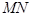 与曲线
与曲线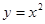 上到直线
上到直线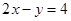 距离最近的点的坐标是______ ___.
距离最近的点的坐标是______ ___.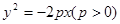 的焦点F恰好是椭圆
的焦点F恰好是椭圆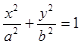 的左焦点,且两曲线的公共点的连线过F,则该椭圆的离心率为
的左焦点,且两曲线的公共点的连线过F,则该椭圆的离心率为 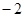 )的抛物线的标准方程为( )
)的抛物线的标准方程为( )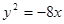
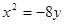
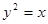 或
或
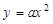 的准线方程是
的准线方程是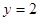 ,则
,则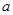 的值为 ____________ .
的值为 ____________ .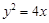 的焦点坐标是 .
的焦点坐标是 .