题目内容
3.已知f(x)是定义在(-1,1)上的奇函数,当x∈(0,1)时,f(x)=2x.(1)求f(x)的解析式;
(2)解不等式:f(a2-1)+f(1-a)>0.
分析 (1)根据函数奇偶性的性质,利用对称性进行求解即可;
(2)利用函数的单调性、奇偶性,即可解不等式.
解答 解:(1)若x∈(-1,0),则-x∈(0,1),
∵当x∈(0,1)时,f(x)=2x,
∴f(-x)=2-x,
∵f(x)是定义在(-1,1)上的奇函数,
∴f(-x)=2-x=-f(x),
则f(x)=-2-x,x<0,
又f(0)=0,
∴f(x)=$\left\{\begin{array}{l}{-{2}^{-x},-1<x<0}\\{0,x=0}\\{{2}^{x},0<x<1}\end{array}\right.$;
(2)∵f(a2-1)+f(1-a)>0,
∴f(a2-1)>f(a-1),
∴$\left\{\begin{array}{l}{-1<a-1<0}\\{0<{a}^{2}-1<1}\end{array}\right.$或1>a2-1>a-1>0或0>a2-1>a-1>-1,
∴1<a<$\sqrt{2}$.
点评 本题主要考查函数解析式的求解,利用函数奇偶性的对称性是解决本题的关键.

练习册系列答案
相关题目
20.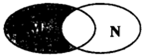 已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
 已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )
已知集合M,N的关系如图所示,若M={x|0<x<2},N={x|1<x<3},则图中阴影部分所表示的集合为( )| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|1<x<2} | D. | {x|2<x<3} |
15.设两相交直线的夹角集合为X,两相交直线l1到l2的角的集合为Y,直线的倾斜角集合为Z,则下面的关系式中正确的是( )
| A. | X=Y$\underset{?}{≠}$Z | B. | X$\underset{?}{≠}$Y=Z | C. | X$\underset{?}{≠}$Y$\underset{?}{≠}$Z | D. | X$\underset{?}{≠}$Z$\underset{?}{≠}$Y |
12.已知复数$z=\frac{5i}{1+2i}$的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.若实数x,y满足$\left\{\begin{array}{l}{x+y≤3}\\{y≥2x}\\{x≥-1}\end{array}\right.$,则(x-3)2+y2的最小值是( )
| A. | $\frac{36}{5}$ | B. | 8 | C. | 20 | D. | 2$\sqrt{5}$ |
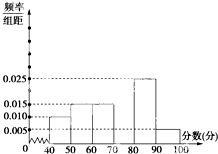 某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题:
某中学团委组织了“弘扬奥运精神,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如下部分频率分布直方图.观察图形给出的信息,回答下列问题: