题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,若直线
,若直线![]() 与函数
与函数![]() 的图象恰有11个不同的公共点,则实数
的图象恰有11个不同的公共点,则实数![]() 的取值范围为____________.
的取值范围为____________.
【答案】![]()
【解析】
根据对称性可知,![]() 时直线
时直线![]() 与函数
与函数![]() 的图象有6个交点,求得函数
的图象有6个交点,求得函数![]() 在
在![]() 上的解析式,并作出图象,可求得临界情况下
上的解析式,并作出图象,可求得临界情况下![]() 的值,进而可求得
的值,进而可求得![]() 的取值范围.
的取值范围.
由题意,函数![]() 和
和![]() 的图象都关于原点对称,则他们的图象交点也关于原点对称,
的图象都关于原点对称,则他们的图象交点也关于原点对称,
又![]() ,可知
,可知![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有6个交点.
的图象有6个交点.
当![]() 时,
时,![]() ,即
,即![]() ,则
,则![]() 时,
时,![]() ,
,
所以,![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
作出函数![]() 在
在![]() 上的图象,
上的图象,
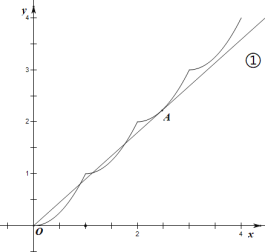
①当直线![]() 与
与![]() 的图象在
的图象在![]() 处相切时,二者图象在
处相切时,二者图象在![]() 上5个交点,
上5个交点,
设切点为点![]() ,联立
,联立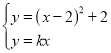 ,可得
,可得![]() ,则
,则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以只有
,所以只有![]() 符合题意;
符合题意;
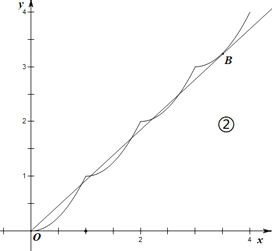
②当直线![]() 与
与![]() 的图象在
的图象在![]() 处相切时,二者图象在
处相切时,二者图象在![]() 上7个交点,
上7个交点,
设切点为点![]() ,联立
,联立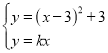 ,可得
,可得![]() ,则
,则![]() ,解得
,解得![]() ,因为
,因为![]() ,所以只有
,所以只有![]() 符合题意;
符合题意;
显然,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 时有6个交点,根据对称性可知,此时直线
时有6个交点,根据对称性可知,此时直线![]() 与函数
与函数![]() 的图象恰有11个不同的公共点.
的图象恰有11个不同的公共点.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目