题目内容
【题目】设甲乙两地相距100海里,船从甲地匀速驶到乙地,已知某船的最大船速是36海里/时:当船速不大于每小时30海里/时,船每小时使用的燃料费用和船速成正比;当船速不小于每小时30海里/时,船每小时使用的燃料费用和船速的平方成正比;当船速为30海里/时,它每小时使用的燃料费用为300元;其余费用(不论船速为多少)都是每小时480元;
(1)试把每小时使用的燃料费用P(元)表示成船速v(海里/时)的函数;
(2)试把船从甲地行驶到乙地所需要的总费用Y表示成船速v的函数;
(3)当船速为每小时多少海里时,船从甲地到乙地所需要的总费用最少?
【答案】(1)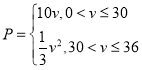 (2)
(2)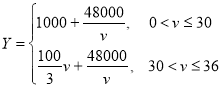 (3)当
(3)当![]() 时,Y有最小值为
时,Y有最小值为![]() (元)
(元)
【解析】
(1)分类讨论,当![]() 时,设
时,设![]() ,从而解得
,从而解得![]() ;再求当
;再求当![]() 时的解析式即可;
时的解析式即可;
(2)分类讨论求总费用![]() 的值,从而利用分段函数写出即可;
的值,从而利用分段函数写出即可;
(3)由分段函数讨论以确定函数的单调性,从而由单调性求最小值即可.
解:(1)由题意,当![]() 时,设
时,设![]() ,
,
由![]() 解得,
解得,![]() ;
;
故![]() ,
,
当![]() 时,设
时,设![]() ,
,
由![]() 解得,
解得,![]() ;
;
故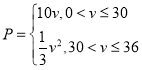 ;
;
(2)当![]() 时,
时,
![]()
当![]() 时,
时,
![]() ;
;
故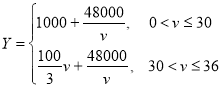 ;
;
(3)当![]() 时,
时,![]() 是减函数,
是减函数,
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]()
则当![]() 时
时![]() ,故
,故![]() 在
在![]() 上是减函数;
上是减函数;
故![]() 在
在![]() 上是减函数,
上是减函数,
故当![]() 时,
时,![]() 有最小值为
有最小值为![]() (元).
(元).

练习册系列答案
相关题目