题目内容
【题目】已知函数![]() ,若存在常数
,若存在常数![]() ,对任意
,对任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为T倍周期函数.
为T倍周期函数.
(1)判断![]() 是否是T倍周期函数,并说明理由;
是否是T倍周期函数,并说明理由;
(2)证明 是T倍周期函数,且T的值是唯一的;
是T倍周期函数,且T的值是唯一的;
(3)若![]() 是2倍周期函数,
是2倍周期函数,![]() ,
,![]() ,
,![]() 表示
表示![]() 的前n项和,
的前n项和,![]() ,若
,若![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
【答案】(1)不是,理由见解析;(2)证明见解析;(3)![]() 或
或![]() .
.
【解析】
(1)假设![]() 是T倍周期函数,推出矛盾即可说明
是T倍周期函数,推出矛盾即可说明![]() 不是T倍周期函数;
不是T倍周期函数;
(2)根据定义,可得到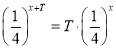 对任意x恒成立,即可求出
对任意x恒成立,即可求出![]() 的值,证明唯一性即可;
的值,证明唯一性即可;
(3)由![]() 是2倍周期函数,可求出
是2倍周期函数,可求出![]() 的奇数项和偶数项,进而可求得
的奇数项和偶数项,进而可求得![]() 和
和![]() ,从而求得
,从而求得![]() 的表达式,然后判断数列
的表达式,然后判断数列![]() 的单调性,可求得
的单调性,可求得![]() ,使得
,使得![]() ,解不等式即可.
,解不等式即可.
(1)不是,
假设![]() 是T倍周期函数,则
是T倍周期函数,则![]() ,
,
则![]() 对任意x恒成立,
对任意x恒成立,
显然![]() 不存在,所以
不存在,所以![]() 不是T倍周期函数.
不是T倍周期函数.
(2)设![]() ,
,
则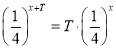 对任意x恒成立,
对任意x恒成立,
即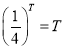 ,则
,则![]() ,
,
下证唯一性:
若![]() ,
,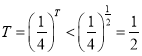 矛盾,
矛盾,
若![]() ,
,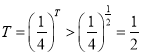 矛盾
矛盾
![]()
![]() 是唯一的;
是唯一的;
(3)![]() ,
,
![]() ,
,
![]() ,
,
…
![]() ,
,
所以![]() ,
,
同理:![]() ,
,
![]()
![]() ,
,
![]() .
.
则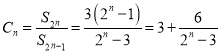 ,
,![]() ,
,![]() ,
,
显然![]() 时,
时,![]() ,
,
因为函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 时,数列
时,数列![]() 是递减数列,
是递减数列,
![]()
![]() ,
,
![]()
![]() 恒成,
恒成,
![]()
![]() ,
,
![]()
![]() ,
,
若![]() 时,则
时,则![]() ,解得
,解得![]() ;
;
若![]() 时,
时,![]() ,解得
,解得![]() ,
,
综上,a的取值范围是![]() 或
或![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目