题目内容
13.在平面直角坐标系xOy中,动点P到两点(-1,0),(1,0)的距离之和等于4,设点P的轨迹为曲线G,直线m:x=1与曲线G交于点M(点M在第一象限).(1)求曲线G的方程;
(2)已知A为曲线G的左顶点,平行于AM的直线l与曲线G相交于B,C两点.判断直线MB,MC是否关于直线m对称,并说明理由.
分析 (1)由椭圆定义可知,点P的轨迹G是以(-1,0),(1,0)为焦点,长半轴长为2的椭圆. 可求得曲线G的方程.
(2)由题意可设直线l:$y=\frac{1}{2}x+n$,n≠1.由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=\frac{1}{2}x+n}\end{array}\right.$得x2+nx+n2-3=0.利用kMB+KMC=0证的结论
解答 解:(1)由椭圆定义可知,点P的轨迹G是以(-1,0),(1,0)为焦点,长半轴长为2的椭圆. 故曲线G的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$. …(4分)
(2)由题意可得点A(-2,0)M(1,$\frac{3}{2}$),…(6分)
所以由题意可设直线l:$y=\frac{1}{2}x+n$,n≠1.…(7分)
设B(x1,y1),C(x2,y2),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=\frac{1}{2}x+n}\end{array}\right.$得x2+nx+n2-3=0.
由题意可得△=n2-4(n2-3)=12-3n2>0,即n∈(-2,2)且n≠1.…(8分)
x1+x2=-n,x1x2=n2-3.…(9分)
因为 ${k}_{MB}+{k}_{MC}=\frac{{y}_{1}-\frac{3}{2}}{{x}_{1}-1}+\frac{{y}_{2}-\frac{3}{2}}{{x}_{2}-1}$ …(10分)
=$\frac{\frac{1}{2}{x}_{1}+n-\frac{3}{2}}{{x}_{1}-1}+\frac{\frac{1}{2}{x}_{2}+n-\frac{3}{2}}{{x}_{2}-1}$=$1+\frac{n-1}{{x}_{1}-1}+\frac{n-1}{{x}_{2}-1}$=1$+\frac{(n-1)({x}_{1}+{x}_{2}-2)}{{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})+1}$
=1-$\frac{(n-1)(n+2)}{{n}^{2}+n-2}=0$,…(13分)
所以直线MB,MC关于直线m对称.…(14分)
点评 本题主要考查直线与圆锥曲线的综合应用题,属高考常考题型,中档题.

| A. | 14 | B. | 16 | C. | 18 | D. | 20 |
| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
 已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1
已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1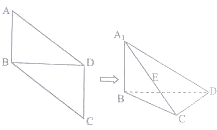 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.