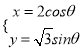题目内容
【题目】设△ABC的内角A,B,C对边分别为a,b,c,已知A=60°,a= ![]() ,sinB+sinC=6
,sinB+sinC=6 ![]() sinBsinC,则△ABC的面积为 .
sinBsinC,则△ABC的面积为 .
【答案】![]()
【解析】解:∵A=60°,a= ![]() , ∴由正弦定理可得:
, ∴由正弦定理可得: ![]() ,可得:sinB=
,可得:sinB= ![]() ,sinC=
,sinC= ![]() ,
,
∵sinB+sinC=6 ![]() sinBsinC,可得:
sinBsinC,可得: ![]() +
+ ![]() =6
=6 ![]() ×
× ![]() ×
× ![]() ,化简可得:b+c=3
,化简可得:b+c=3 ![]() bc,
bc,
∴两边平方可得:b2+c2+2bc=18b2c2 , ①
又∵由余弦定理a2=b2+c2﹣2bccosA,可得:3=b2+c2﹣bc,②
∴联立①②可得:6b2c2﹣bc﹣1=0,解得:bc= ![]() ,或﹣
,或﹣ ![]() (舍去),
(舍去),
∴△ABC的面积S= ![]() bcsinA=
bcsinA= ![]() =
= ![]() .
.
故答案为: ![]() .
.
由已知及正弦定理可得sinB= ![]() ,sinC=
,sinC= ![]() ,化简已知等式可得b+c=3
,化简已知等式可得b+c=3 ![]() bc,两边平方可得:b2+c2+2bc=18b2c2 , 又由余弦定理可得3=b2+c2﹣bc,从而联立即可解得bc的值,进而利用三角形面积公式即可计算得解.
bc,两边平方可得:b2+c2+2bc=18b2c2 , 又由余弦定理可得3=b2+c2﹣bc,从而联立即可解得bc的值,进而利用三角形面积公式即可计算得解.

【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
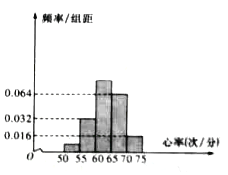
(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 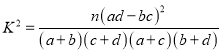 ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到如图频率分布表:
),得到如图频率分布表:
分组(身高) |
|
|
|
|
(Ⅰ)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(Ⅱ)在(Ⅰ)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
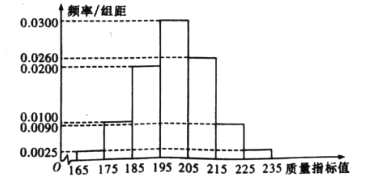
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?