题目内容
10.给出下列四个命题:①a>β的充分不必要条件是sinα>sinβ;
②若a,b∈R,ab<0,则$\frac{b}{a}$+$\frac{a}{b}$≤-2;
③已知点A(-1,0),B(1,0),若|PA|-|PB|=2,则动点P的轨迹为双曲线的一支;
④若a≠b,则a3+b3>a2b+ab2
其中所有真命题的序号是②.
分析 ①结合三角函数的性质进行判断即可;
②根据所给式子的特点,结合ab<0,利用不等式求解;
③利用双曲线的定义直接判断,注意限制条件即“距离差的绝对值小于两定点间的距离”;
④作差,根据a≠b判断符号.
解答 解:对于①,取α=2π,β=0,由此可见,“α>β”是“sinα>sinβ”的既不充分也不必要条件,故①为假;
对于②,因为ab<0,所以$\frac{b}{a}+\frac{a}{b}=-(-\frac{b}{a}-\frac{a}{b})≤-2\sqrt{(-\frac{b}{a})×(\frac{a}{b})}=-2$,故②为真;
对于③,因为|PA|-|PB|=|AB|=2,所以P点的轨迹是以B为起点,方向为AB方向的射线,故③错误;
对于④,由已知可得a3+b3-a2b-ab2=(a-b)2(a+b)(*).
因为a≠b,所以(a-b)2>0,但a+b的符号不确定,因此(*)式的符号不确定,所以未必有原式成立.故④为假.
故答案为②
点评 命题真假的判断主要是以概念的考查为主,因此须结合相关的概念、定义等来处理,注意对条件的准确理解.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
18.已知命题p:对任意x∈R,总有3x>0;命题q:“x>2”是“x>4”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧¬q | C. | ¬p∧q | D. | p∧¬q |
5.如图是一个几何体的三视图,其中正(主)视图、侧(左)视图都是矩形,则该几何体的体积是( )
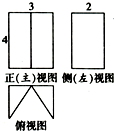

| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
2.已知集合A={x|x2>1},集合B={x|x(x-2)<0},则A∩B=( )
| A. | {x|1<x<2} | B. | {x|x>2} | C. | {x|0<x<2} | D. | {x|x≤1,或x≥2} |
 为丰富市民的文化生活,市政府计划在一块半径为200m,圆心角为120°的扇形地上建造市民广场.规划设计如图:内接梯形ABCD区域为运动休闲区,其中A,B分别在半径OP,OQ上,C,D在圆弧$\widehat{PQ}$上,CD∥AB;△OAB区域为文化展示区,AB长为$50\sqrt{3}$m;其余空地为绿化区域,且CD长不得超过200m.
为丰富市民的文化生活,市政府计划在一块半径为200m,圆心角为120°的扇形地上建造市民广场.规划设计如图:内接梯形ABCD区域为运动休闲区,其中A,B分别在半径OP,OQ上,C,D在圆弧$\widehat{PQ}$上,CD∥AB;△OAB区域为文化展示区,AB长为$50\sqrt{3}$m;其余空地为绿化区域,且CD长不得超过200m.