题目内容
已知函数
(1)求 在点
在点 处的切线方程;
处的切线方程;
(2)若存在 ,使
,使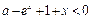 成立,求
成立,求 的取值范围;
的取值范围;
(3)当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
解(1)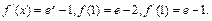
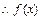 在
在 处的切线方程为
处的切线方程为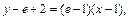
即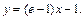
(2)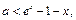 即
即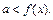
令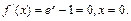
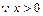 时,
时,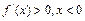 时,
时,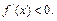
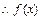 在
在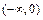 上减,在
上减,在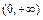 上增.
上增.
又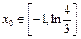 时,
时,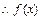 的最大值在区间端点处取到.
的最大值在区间端点处取到.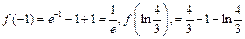 ,
,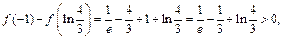
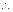
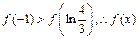 在
在 上最大值为
上最大值为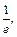
故 的取值范围是
的取值范围是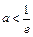 ,
,
(3)由已知得 时,
时,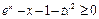 恒成立,
恒成立,
设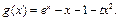
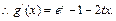
由(2)知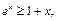 当且仅当
当且仅当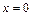 时等号成立,
时等号成立,
故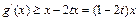 ,从而当
,从而当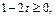
即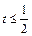 时,
时,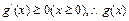 为增函数,又
为增函数,又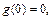
于是当 时,
时,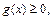 即
即 ,
,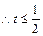 时符合题意.
时符合题意.
由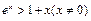 可得
可得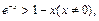 从而当
从而当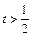 时,
时,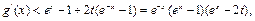
故当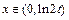 时,
时,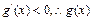 为减函数,又
为减函数,又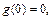
于是当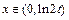 时,
时,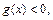 即
即
故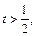 不符合题意.综上可得
不符合题意.综上可得 的取值范围为
的取值范围为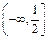
解析

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 (
( 为实常数)。
为实常数)。 时,求函数
时,求函数 的单调区间;
的单调区间; 在区间
在区间 上无极值,求
上无极值,求 且
且 ,求证:
,求证:  .
. 图象的对称中心为
图象的对称中心为 ,且
,且 的极小值为
的极小值为 .
. ,若
,若 有三个零点,求实数
有三个零点,求实数 的取值范围;
的取值范围; ,当
,当 时,使函数
时,使函数
 ,其中
,其中 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 上,
上, 恒成立,求a的取值范围.
恒成立,求a的取值范围. 为奇函数,且
为奇函数,且 在
在 处取得极大值2.
处取得极大值2. 的解析式;
的解析式; ,求函数
,求函数 的单调区间。
的单调区间。 .
. 在
在 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围;
的取值范围; 时,
时, 上的最小值为
上的最小值为 ,求
,求 与曲线
与曲线 交于点
交于点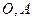 .直线
.直线 与曲线
与曲线 分别相交于点
分别相交于点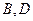 .
. 的面
的面 积
积 与
与 的函数关系
的函数关系 ;
; 的单调性,并求
的单调性,并求
 ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线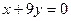 垂直
垂直 的值
的值 )若函数
)若函数 的取值范围。
的取值范围。 x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0. )求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.
)求函数f(x)的单调区间,并求出f(x)在区间[-2,4]上的最大值.