题目内容
已知函数 为奇函数,且
为奇函数,且 在
在 处取得极大值2.
处取得极大值2.
(1)求函数 的解析式;
的解析式;
(2)记 ,求函数
,求函数 的单调区间。
的单调区间。
解:(1)由 (
( ≠0)为奇函数,
≠0)为奇函数,
∴ ,代入得,
,代入得, ………………………………………………1分
………………………………………………1分
∴ ,且
,且 在
在 取得极大值2.
取得极大值2.
∴ 解得
解得 ,
, ,∴
,∴ …………4分
…………4分
(2)∵ ,定义域为
,定义域为
∴ ……
…… …………………………………5分
…………………………………5分
1°当 ,即
,即 时,
时, ,函数在
,函数在 上单调递减;………7分
上单调递减;………7分
2°当 ,
, ,∵
,∵ ,∴
,∴
∴函数在 上单调递减; ………………………………………………………9分
上单调递减; ………………………………………………………9分
3°当 ,
, ,令
,令 ,∵
,∵ ,
,
∴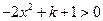 ,解得
,解得 ,结合
,结合 ,得
,得 ……11分[来源:Z。xx。k.Com]
……11分[来源:Z。xx。k.Com]
令 ,解得
,解得 ………………………………………12分
………………………………………12分
∴ 时,函数的单调递增区间为
时,函数的单调递增区间为 ,递减区间为
,递减区间为 ,………13分
,………13分
综上,当 时,函数的单调递减区间为
时,函数的单调递减区间为 ,无单调递增区间,
,无单调递增区间,
当 时,函数的单调递增区间为
时,函数的单调递增区间为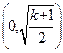 ,递减区间为
,递减区间为 …14分
…14分
解析

练习册系列答案
相关题目

 的值;
的值; 过原点的切线与函数
过原点的切线与函数 的图像有两个交点,试求b的取值范围.
的图像有两个交点,试求b的取值范围. ,其中
,其中
 若
若 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值; 求
求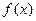 =
= ,
, .
. 在区间
在区间 上的值域T;
上的值域T; ,对任意给定的集合T中的元素t,在区间
,对任意给定的集合T中的元素t,在区间 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立.若存在,求出
成立.若存在,求出
 (
( ).
). 时,求
时,求 在点
在点 处的切线方程;
处的切线方程; 上的最小值.
上的最小值.
 在点
在点 处的切线方程;
处的切线方程; ,使
,使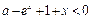 成立,求
成立,求 的取值范围;
的取值范围; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.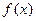 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时
时
 ,使得当
,使得当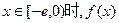 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出
 其中
其中
 的单调区间;
的单调区间; (
( )(
)( 为自然对数的底数)
为自然对数的底数) 的极值
的极值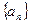 ,
, (
( )
)

 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由