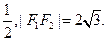题目内容
如图,已知中心在原点,焦点在x轴上的椭圆经过点(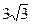 ,
,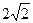 ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
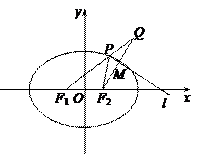
(1)求椭圆的标准方程;
(2)设P是椭圆上不同于左右顶点的动点,延长F1P至Q,使Q、F2关于∠F1PF2的外角平分线l对称,求F2Q与l的交点M的轨迹方程.
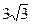 ,
,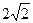 ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.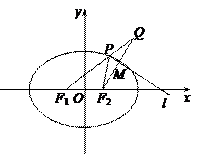
(1)求椭圆的标准方程;
(2)设P是椭圆上不同于左右顶点的动点,延长F1P至Q,使Q、F2关于∠F1PF2的外角平分线l对称,求F2Q与l的交点M的轨迹方程.
解:(1)设椭圆的方程为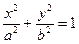 (a>b>0),半焦距为c,则a2-b2=c2,
(a>b>0),半焦距为c,则a2-b2=c2,
∵ 椭圆经过点(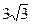 ,
,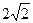 ),
),
∴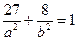 .
.
又∵ 它的左焦点F将长轴分成2∶1,
∴ (a+c)∶(a-c)=2∶1,整理得a=3c.
联立①②③,即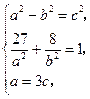 解得a2=36,b2=32,c2=4.
解得a2=36,b2=32,c2=4.
∴ 椭圆的标准方程为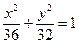 . ……………………4分
. ……………………4分
(2)∵ Q、F2关于∠F1PF2的外角平分线l对称,
∴ |PQ|=|PF2|,且M是F2Q的中点.
 由椭圆的定义知|PF1|+|PF2|=12,
由椭圆的定义知|PF1|+|PF2|=12,
∴ |PF1|+|PQ|=12,即|F1Q|=12,
∴ Q的轨迹是以F1(-2,0)为圆心,12为半径的圆(除去与x轴的两个交点),其轨迹方程为(x+2)2+y2=144(y≠0). …………………7分
设M(x,y),Q(a,b),由(1)知F2(2,0),
∴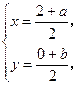 可整理得a=2x-2,b=2y,
可整理得a=2x-2,b=2y,
∵ Q(a,b)在圆(x+2)2+y2=144(y≠0)上运动,
∴ (2x-2+2)2+(2y)2=144,即x2+y2=36.
∴ M的轨迹方程为x2+y2=36(y≠0). ……………………10分
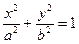 (a>b>0),半焦距为c,则a2-b2=c2,
(a>b>0),半焦距为c,则a2-b2=c2,∵ 椭圆经过点(
 ,
,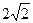 ),
),∴
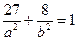 .
.又∵ 它的左焦点F将长轴分成2∶1,
∴ (a+c)∶(a-c)=2∶1,整理得a=3c.
联立①②③,即
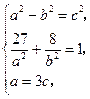 解得a2=36,b2=32,c2=4.
解得a2=36,b2=32,c2=4.∴ 椭圆的标准方程为
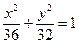 . ……………………4分
. ……………………4分(2)∵ Q、F2关于∠F1PF2的外角平分线l对称,
∴ |PQ|=|PF2|,且M是F2Q的中点.
 由椭圆的定义知|PF1|+|PF2|=12,
由椭圆的定义知|PF1|+|PF2|=12,∴ |PF1|+|PQ|=12,即|F1Q|=12,
∴ Q的轨迹是以F1(-2,0)为圆心,12为半径的圆(除去与x轴的两个交点),其轨迹方程为(x+2)2+y2=144(y≠0). …………………7分
设M(x,y),Q(a,b),由(1)知F2(2,0),
∴
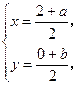 可整理得a=2x-2,b=2y,
可整理得a=2x-2,b=2y,∵ Q(a,b)在圆(x+2)2+y2=144(y≠0)上运动,
∴ (2x-2+2)2+(2y)2=144,即x2+y2=36.
∴ M的轨迹方程为x2+y2=36(y≠0). ……………………10分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
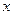 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为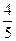 ,且过点
,且过点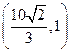 (题干自编)
(题干自编)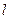 分别切椭圆C与圆
分别切椭圆C与圆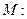
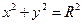 (其中
(其中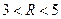 )于
)于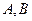 两点,求
两点,求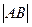 的最大值。
的最大值。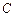 :
: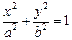 (
(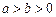 ),其焦距为
),其焦距为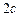 ,若
,若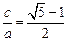 (
( ),则称椭圆
),则称椭圆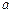 、
、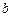 、
、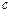 成等比数列.
成等比数列.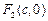 ,
,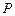 为椭圆
为椭圆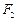 、
、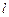 ,使
,使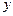 轴的交点
轴的交点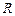 满足
满足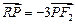 ?若存在,求直线
?若存在,求直线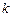 ;若不存在,请说明理由.
;若不存在,请说明理由.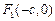 、
、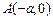 、
、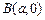 、
、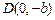 、
、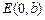 为顶点的菱形
为顶点的菱形 的内切圆过焦点
的内切圆过焦点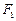 、
、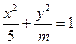 表示是焦点在y轴上的椭圆;q:三次函数
表示是焦点在y轴上的椭圆;q:三次函数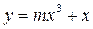
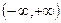 内单调递增,.求使“
内单调递增,.求使“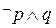 ”为真命题的实数m的取值范围.
”为真命题的实数m的取值范围.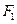 、
、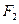 分别是椭圆C:
分别是椭圆C: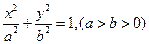 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过 两端点
两端点 与
与 的周长是
的周长是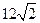 .
.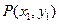 ,
,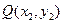 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段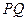 的中点为
的中点为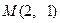 .
. 、
、 ,试问四点
,试问四点 、
、 、
、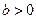 ,椭圆方程为
,椭圆方程为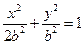 ,抛物线方程为
,抛物线方程为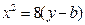 .如图所示,过点
.如图所示,过点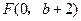 作
作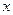 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为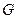 ,已知抛物线在点
,已知抛物线在点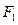 .
.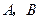 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点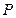 ,使得
,使得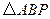 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).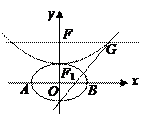
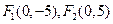 ,点
,点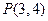
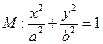
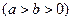 的离心率为
的离心率为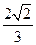 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为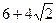 .
.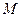 的方程;
的方程;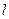 与椭圆
与椭圆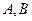 两点,且以
两点,且以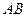 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点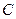 ,
,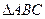 面积的最大值.
面积的最大值.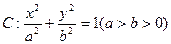 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=