题目内容
((本小题满分12分)
椭圆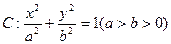 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=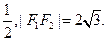
(I)求椭圆C的方程。
(II)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由。
椭圆
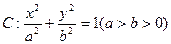 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥F1F2,且|PF1|=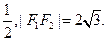
(I)求椭圆C的方程。
(II)以此椭圆的上顶点B为直角顶点作椭圆的内接等腰直角三角形ABC,这样的直角三角形是否存在?若存在,请说明有几个;若不存在,请说明理由。
解: (Ⅰ)

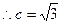
又

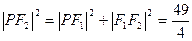 ,
,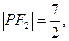
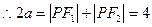 则
则 ,
,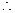

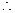 所求椭圆方程为
所求椭圆方程为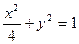 . …………………………………………6分
. …………………………………………6分(Ⅱ)设能构成等腰直角三角形
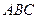 ,其中
,其中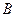 (0,1),由题意可知,直角边
(0,1),由题意可知,直角边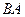 ,
,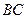 不可能垂直或平行于x轴,故可设
不可能垂直或平行于x轴,故可设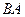 边所在直线的方程为
边所在直线的方程为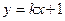 (不妨设
(不妨设 ),则
),则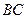 边所在直线的方程为
边所在直线的方程为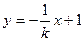 ,由
,由 ,得A
,得A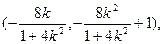
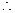
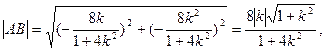 ………………………………9分
………………………………9分用
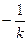 代替上式中的
代替上式中的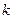 ,得
,得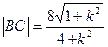 ,由
,由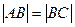 ,得
,得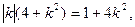
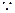
 ,
, 解得:
解得: 或
或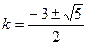 ,故存在三个内接等腰直角三角形.……12分
,故存在三个内接等腰直角三角形.……12分略

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
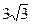 ,
,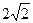 ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.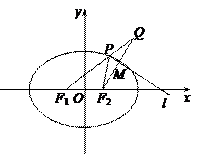
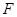 为双曲线
为双曲线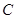 :
: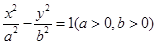 的右焦点,
的右焦点,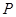 为双曲线
为双曲线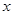 轴上方,
轴上方,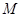 为直线
为直线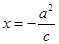 上一点,
上一点,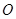 为坐标原点,已知
为坐标原点,已知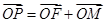 ,
,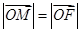 ,则双曲线
,则双曲线



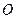 ,焦点在
,焦点在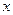 轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.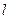 过
过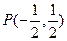 且与椭圆相交于A,B两点,当P是AB的中点时,
且与椭圆相交于A,B两点,当P是AB的中点时,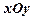 中,椭圆
中,椭圆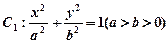 的左、右焦点分别为
的左、右焦点分别为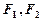 . 其中
. 其中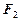 也是抛物线
也是抛物线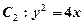 的焦点,点
的焦点,点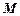 为
为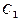 与
与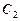 在第一象限的交点,且
在第一象限的交点,且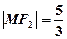
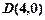 的直线
的直线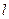 与
与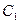 交于不同的两点
交于不同的两点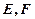 .
.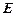 在
在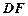 之间,试求
之间,试求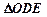 与
与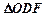 面积之比的取值范围.(O为坐标原点)
面积之比的取值范围.(O为坐标原点)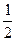
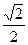
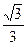
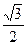
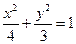 的左、右焦点,曲线C是坐标原点为顶
的左、右焦点,曲线C是坐标原点为顶 点,
点,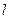 交
交 曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设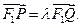
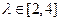 ,求直线
,求直线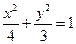 的左、右焦点,曲线C是坐标原点为顶
的左、右焦点,曲线C是坐标原点为顶 点,
点,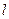 交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设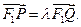
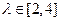 ,求直线
,求直线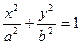
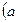 >
>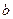 >
>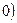 与直线
与直线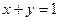 交于
交于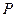 、
、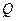 两点,且
两点,且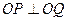 ,其
,其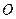 为坐标原点。
为坐标原点。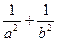 的值;
的值;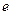 满足
满足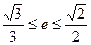 ,求椭圆长轴的取值范围。
,求椭圆长轴的取值范围。