Question

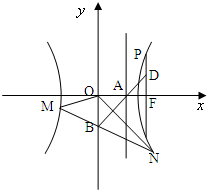（2008•湖北模拟）如图，已知双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)，其右准线交x轴于点A，双曲线虚轴的下端点为B．过双曲线的右焦点F（c，0）作垂直于x轴的直线交双曲线于点P，若点D满足2

OD

=

OF

+

OP

(O为原点)，且

AB

=λ

AD

(λ≠0)．
（1）求双曲线的离心率；
（2）若a=2，过点B作直线l分别交双曲线的左支、右支于M、N两点，且△OMN的面积S_△OMN=2

6

，求l的方程．

Answer 1

分析：（1）欲求双曲线的离心率，只需找到含a，c的齐次式，由已知，易求P点坐标，根据2

OD

=

OF

+

OP

(O为原点)，可判断D点为FP的中点，再根据

AB

=λ

AD

(λ≠0)可找到a，b的关系，进而转化为含a，c的等式，即可求出离心率e的值．
（2）当a=2时，根据（1）中所求离心率，可求出b的值，进而求出双曲线方程，根据直线MN过B点，设出直线MN的方程，与双曲线方程联立，解出x₁+x₂，x₁x₂，△OMN被y轴分成两个三角形，分别求出面积，再相加，即为△OMN的面积，让其等于题目中所给的值，可得到关于直线l的斜率k的方程，解出k即可．

解答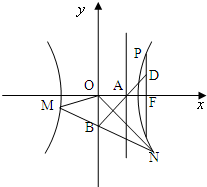：解：（1）∵B（0，-b）A(

a2

c

，0)，易求得P(c，

b2

a

)
∵2

OD

=

OF

+

OP

，即D为线段FP的中点．，
∴D(c，

b2

2a

)
又

AB

=λ

AD

，即A、B、D共线．
而  

AB

=(-

a2

c

，-b)，

AD

=(c-

a2

c

，

b2

2a

)，
∴(c-

a2

c

)•(-b)=(-

a2

c

)(

b2

2a

)，得a=2b，
∴e=

c

a

=

1+( b a )2

=

1+ 1 4

=

5

2

（2）∵a=2，而e=

5

2

，∴b²=1，
故双曲线的方程为

x2

4

-y2=1…①
∴B、的坐标为（0，-1）

设l的方程为y=kx-1…②
②代入①得（1-4k²）x²+8kx-8=0
由题意得：

1-4k2≠0 △=64k2+32(1-4k2)＞0 x1•x2= 8 4k2-1 ＜0

得：k2＜

1

4

设M、N的坐标分别为（x₁，y₁）、（x₂，y₂）
则x1+x2=

8k

4k2-1

而S△OMN=

1

2

|OB|(|x1|+|x2|)=

1

2

|x1-x2|=

1

2

(x1+x2)2-4x1•x2

=

1

2

( 8k 4k2-1 )2- 32 4k2-1

=

2 2 • 1-2k2

1-4k2

=2

6

整理得24k⁴-11k²+1=0，解得：k2=

1

8

或k2=

1

3

（舍去）
∴所求l的方程为y=±

2

4

x-1

点评：本题主要考查了双曲线离心率的求法，以及直线与 双曲线位置关系的应用．