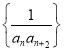题目内容
【题目】函数f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形. 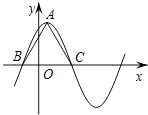
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)= ![]() ,且x0∈(﹣
,且x0∈(﹣ ![]() ,
, ![]() ),求f(x0+1)的值.
),求f(x0+1)的值.
【答案】
(1)解:由已知得f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3
sinωx﹣3
=3cosωx+ ![]() sinωx=2
sinωx=2 ![]() sin(ωx+
sin(ωx+ ![]() )
)
又△ABC为正三角形,且高为2 ![]() ,可得BC=4.
,可得BC=4.
∴函数f(x)的最小正周期为8,即 ![]() =8,
=8,
解得ω= ![]() ,∴f(x)=2
,∴f(x)=2 ![]() sin(
sin( ![]() x+
x+ ![]() ),
),
∴函数f(x)的值域为:[﹣2 ![]() ,2
,2 ![]() ];
];
(2)解:∵f(x0)= ![]() ,
,
∴2 ![]() sin(
sin( ![]() x0+
x0+ ![]() )=
)= ![]() ,
,
故sin( ![]() x0+
x0+ ![]() )=
)= ![]() ,
,
∵x0∈(﹣ ![]() ,
, ![]() ),∴
),∴ ![]() x0+
x0+ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),
),
∴cos( ![]() x0+
x0+ ![]() )=
)= ![]() =
= ![]()
∴f(x0+1)=2 ![]() sin(
sin( ![]() x0+
x0+ ![]() +
+ ![]() )
)
=2 ![]() ×
× ![]() [sin(
[sin( ![]() x0+
x0+ ![]() )+cos(
)+cos( ![]() x0+
x0+ ![]() )]=
)]= ![]()
【解析】(1)变形可得f(x)=2 ![]() sin(ωx+
sin(ωx+ ![]() ),由又由三角形的知识和周期公式可得ω=
),由又由三角形的知识和周期公式可得ω= ![]() ,由振幅的意义可得值域;(2)由已知和(1)的解析式可得sin(
,由振幅的意义可得值域;(2)由已知和(1)的解析式可得sin( ![]() x0+
x0+ ![]() )=
)= ![]() ,进而由角的范围和同角三角函数基本关系可得cos(
,进而由角的范围和同角三角函数基本关系可得cos( ![]() x0+
x0+ ![]() )=
)= ![]() ,代入f(x0+1)=2
,代入f(x0+1)=2 ![]() sin(
sin( ![]() x0+
x0+ ![]() +
+ ![]() )=2
)=2 ![]() ×
× ![]() [sin(
[sin( ![]() x0+
x0+ ![]() )+cos(
)+cos( ![]() x0+
x0+ ![]() )]计算可得.
)]计算可得.

练习册系列答案
相关题目