题目内容
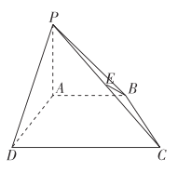
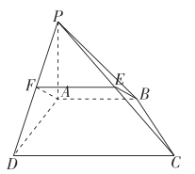
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,先证明四边形
,先证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,只需证
,只需证![]() 平面
平面![]() 即可,而由已知易证
即可,而由已知易证![]() 平面
平面![]() ,从而可证得
,从而可证得![]() ,而由等腰三角形的性质可证得
,而由等腰三角形的性质可证得![]() ,由此可证得
,由此可证得![]() 平面
平面![]() ;
;
(2)先在![]() 中利用勾股定理求出
中利用勾股定理求出![]() 的长,再在
的长,再在![]() 中,求出
中,求出![]() ,从而可得
,从而可得![]() 的长,而
的长,而![]() 为
为![]() 的中点,所以
的中点,所以![]() ,在
,在![]() 中,再利用勾股定理求出
中,再利用勾股定理求出![]() ,而由(1)可知
,而由(1)可知![]() 平面
平面![]() ,所以
,所以![]() ,代值可得答案.
,代值可得答案.
(1)证明:如下图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
又![]() 为
为![]() 的中点,则
的中点,则![]() 是
是![]() 的中位线.
的中位线.
所以![]() 且
且![]() .
.
又![]() 且
且![]() ,
,
所以![]() 且
且![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() ,
,
所以由勾股定理得![]() ,
,![]() ,
,![]() .
.
所以![]() .
.
所以![]() .
.
由(1)得,![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() .
.
由(1)得,![]() 平面
平面![]() ,
,
所以![]() .
.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,将用电量的数据绘制成频率分布直方图如下.
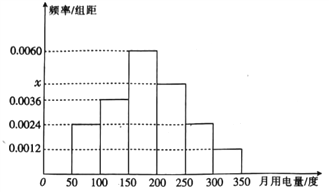
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;
的值并估计这50户用户的平均用电量;
(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图:
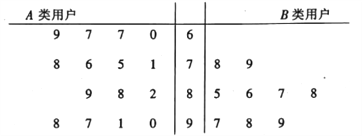
①从![]() 类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
类用户中任意抽取3户,求恰好有2户打分超过85分的概率;
②若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| <>0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
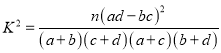 ,
, ![]() .
.