Question

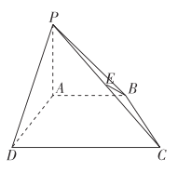
【题目】如图，在四棱锥P－ABCD中，底面ABCD为直角梯形，AB∥CD，AB⊥AD，PA⊥平面ABCD，E是棱PC上一点.

（1）证明：平面ADE⊥平面PAB.

（2）若PE＝4EC，O为点E在平面PAB上的投影，，AB＝AP＝2CD＝2，求四棱锥P－ADEO的体积.

Answer 1

【答案】（1）证明见解析（2）

【解析】

(1) 由PA⊥平面ABCD,可得PA⊥AD，又AB⊥AD,则AD⊥平面PAB即可证得结论;

(2) 取AB的中点F可得CF⊥AB,进而有CF⊥面PAB,即EO∥CF,可知O点在线段PF上,由已知可得PO＝4OF即,因为,则，因为,代入即可得出结果.

（1）证明：因为PA⊥平面ABCD，平面ABCD，所以PA⊥AD，

又AB⊥AD，PA∩AB＝A，所以AD⊥平面PAB，

又平面ADE，所以平面ADE⊥平面PAB；

（2）解：取AB的中点F，

所以CF∥AD，则CF⊥AB，

又PA⊥CF，PA∩AB＝A，所以CF⊥面PAB，

则EO∥CF，即O点在线段PF上，

又PE＝4EC，所以PO＝4OF，，

则，，

，.