题目内容
【题目】某饲料厂原有陈粮10吨,又购进新粮x吨,现将粮食总库存量的一半精加工为饲料.若被精加工的新粮最多可用![]() 吨,被精加工的陈粮最多可用y2吨,记
吨,被精加工的陈粮最多可用y2吨,记![]() ,则函数
,则函数![]() 的图象为( )
的图象为( )
A.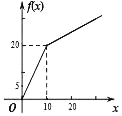 B.
B.
C.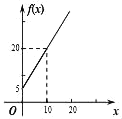 D.
D.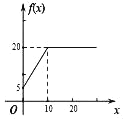
【答案】B
【解析】
根据条件,利用特殊值分别验证当![]() ,10,20时,函数图象的对应值,利用排除法进行求解即可.
,10,20时,函数图象的对应值,利用排除法进行求解即可.
若![]() ,则此时库存为10吨,则库存的一半为5吨加工成饲料,则
,则此时库存为10吨,则库存的一半为5吨加工成饲料,则![]() ,
,![]() ,
,
此时![]() ,排除A,
,排除A,
若![]() ,则此时库存为
,则此时库存为![]() 吨,则库存的一半为10吨加工成饲料,
吨,则库存的一半为10吨加工成饲料,
若全部被加工的是陈粮,则![]() ,若全部被加工的是新粮,则
,若全部被加工的是新粮,则![]() ,
,
此时![]() ,
,
若![]() ,则此时库存为
,则此时库存为![]() 吨,则库存的一半为15吨加工成饲料,
吨,则库存的一半为15吨加工成饲料,
若全部被加工的是陈粮,则y2=10,若全部被加工的是新粮,则![]() ,
,
此时![]() ,排除D,
,排除D,
因为![]() ,
,![]() ,
,![]() 三点不共线,所以不可能是直线,故排除C,
三点不共线,所以不可能是直线,故排除C,
故选:B.

【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项.共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,武汉市很多单位和部门都开展了丰富多彩的宣传和教育活动,努力让大家更多的了解军运会的相关知识,并倡议大家做文明公民.武汉市体育局为了解广大民众对军运会知识的知晓情况,在全市开展了网上问卷调查,民众参与度极高,现从大批参与者中随机抽取200名幸运参与者,他们得分(满分100分)数据,统计结果如下:
组别 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
(1)若此次问卷调查得分整体服从正态分布,用样本来估计总体,设![]() ,
,![]() 分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求
分别为这200人得分的平均值和标准差(同一组数据用该区间中点值作为代表),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整数),并计算
的值四舍五入取整数),并计算![]() ;
;
(2)在(1)的条件下,为感谢大家参与这次活动,市体育局还对参加问卷调查的幸运市民制定如下奖励方案:得分低于![]() 的可以获得1次抽奖机会,得分不低于
的可以获得1次抽奖机会,得分不低于![]() 的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为
的可获得2次抽奖机会,在一次抽奖中,抽中价值为15元的纪念品A的概率为![]() ,抽中价值为30元的纪念品B的概率为
,抽中价值为30元的纪念品B的概率为![]() .现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
.现有市民张先生参加了此次问卷调查并成为幸运参与者,记Y为他参加活动获得纪念品的总价值,求Y的分布列和数学期望,并估算此次纪念品所需要的总金额.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
【题目】2017年冬,北京雾霾天数明显减少,据环保局统计三个月的空气质量,达到优良的天数超过![]() 天,重度污染的天数仅有
天,重度污染的天数仅有![]() 天,主要原因是政府对治理雾霾采取有效措施.如:(1)减少机动车尾气排放(2)实施煤改电或煤改气工程(3)关停了大量的排污企业(4)部分企业季节性停产.为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取
天,主要原因是政府对治理雾霾采取有效措施.如:(1)减少机动车尾气排放(2)实施煤改电或煤改气工程(3)关停了大量的排污企业(4)部分企业季节性停产.为了解农村地区实施煤改气工程后天然气的使用从某乡镇随机抽取![]() 户,进行月均用气量调查,得到的用气量数据均在区间
户,进行月均用气量调查,得到的用气量数据均在区间![]() 内,表如下
内,表如下
分组 | 频数 | 频率 |
| 14 | 0.14 |
|
|
|
| 55 | 0.55 |
| 4 | 0.04 |
| 2 | 0.02 |
合计 | 100 | 1 |
(1)求![]() 和
和![]() 值,若同组内的每个数据用该组区间中点值代替,估计该乡镇每户平均用气量;
值,若同组内的每个数据用该组区间中点值代替,估计该乡镇每户平均用气量;
(2)从样本调查的用气量![]() 和
和![]() 的用户组中任选2户,进行燃气使用满意度调查,求2户用气量处于不同区间的概率.
的用户组中任选2户,进行燃气使用满意度调查,求2户用气量处于不同区间的概率.
【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:
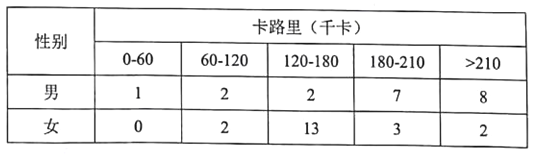
(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
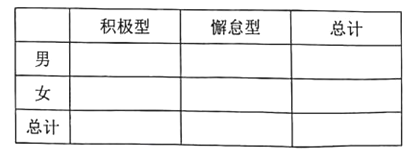
(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 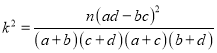 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.

成绩分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
高二
(1)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(2)在抽取的学生中,从成绩为![]() 的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率.
的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率.