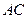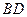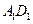题目内容
如图所示,已知PA⊥矩形ABCD所在平面,
M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;
(2)若∠PDA=45°.求证:MN⊥平面PCD.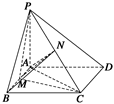
M,N分别是AB,PC的中点.
(1)求证:MN⊥CD;
(2)若∠PDA=45°.求证:MN⊥平面PCD.

证明略
(1)连接AC,AN,BN,
∵PA⊥平面ABCD,∴PA⊥AC,
在Rt△PAC中,N为PC中点,
∴AN=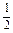 PC.
PC.
∵PA⊥平面ABCD,
∴PA⊥BC,又BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB,∴BC⊥PB,
从而在Rt△PBC中,BN为斜边PC上的中线,
∴BN=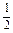 PC.
PC.
∴AN=BN,
∴△ABN为等腰三角形,
又M为底边的中点,∴MN⊥AB,
又∵AB∥CD,∴MN⊥CD.
(2)连接PM、CM,∵∠PDA=45°,PA⊥AD,∴AP=AD.
∵四边形ABCD为矩形.
∴AD=BC,∴PA=BC.
又∵M为AB的中点,∴AM=BM.
而∠PAM=∠CBM=90°,∴PM=CM.
又N为PC的中点,∴MN⊥PC.
由(1)知,MN⊥CD,PC∩CD=C,
∴MN⊥平面PCD.
∵PA⊥平面ABCD,∴PA⊥AC,
在Rt△PAC中,N为PC中点,
∴AN=
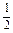 PC.
PC.∵PA⊥平面ABCD,
∴PA⊥BC,又BC⊥AB,PA∩AB=A,
∴BC⊥平面PAB,∴BC⊥PB,
从而在Rt△PBC中,BN为斜边PC上的中线,
∴BN=
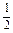 PC.
PC.∴AN=BN,
∴△ABN为等腰三角形,
又M为底边的中点,∴MN⊥AB,
又∵AB∥CD,∴MN⊥CD.
(2)连接PM、CM,∵∠PDA=45°,PA⊥AD,∴AP=AD.
∵四边形ABCD为矩形.
∴AD=BC,∴PA=BC.
又∵M为AB的中点,∴AM=BM.
而∠PAM=∠CBM=90°,∴PM=CM.
又N为PC的中点,∴MN⊥PC.
由(1)知,MN⊥CD,PC∩CD=C,
∴MN⊥平面PCD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
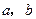 是不共面的直线,且
是不共面的直线,且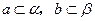 ,
,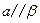 ,
,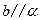 ,求证:
,求证: .
.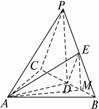
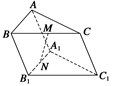
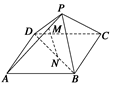
 正方形
正方形 ,
,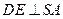 于
于 ,
,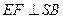 于
于 .
. 交
交 于
于 ,(1)求证:
,(1)求证: ; (2)求证:
; (2)求证: 面
面 .
.
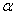 和共面的直线m、n,下列命题中真命题是 ( )
和共面的直线m、n,下列命题中真命题是 ( )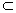

 中,若
中,若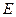 是
是 的中点,则直线
的中点,则直线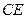 垂直于( )
垂直于( )