题目内容
设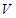 是已知平面
是已知平面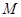 上所有向量的集合,对于映射
上所有向量的集合,对于映射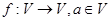 ,记
,记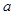 的象为
的象为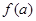 。若映射
。若映射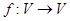 满足:对所有
满足:对所有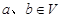 及任意实数
及任意实数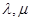 都有
都有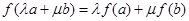 ,则
,则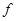 称为平面
称为平面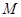 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设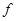 是平面
是平面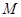 上的线性变换,
上的线性变换,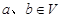 ,则
,则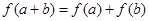 ;
;
②若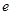 是平面
是平面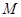 上的单位向量,对
上的单位向量,对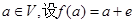 ,则
,则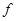 是平面
是平面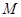 上的线性变换;
上的线性变换;
③对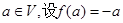 ,则
,则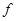 是平面
是平面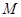 上的线性变换;
上的线性变换;
④设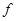 是平面
是平面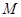 上的线性变换,
上的线性变换,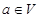 ,则对任意实数
,则对任意实数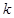 均有
均有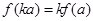 。
。
其中的真命题是 .(写出所有真命题的编号)
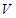 是已知平面
是已知平面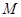 上所有向量的集合,对于映射
上所有向量的集合,对于映射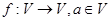 ,记
,记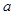 的象为
的象为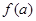 。若映射
。若映射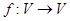 满足:对所有
满足:对所有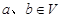 及任意实数
及任意实数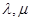 都有
都有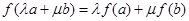 ,则
,则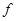 称为平面
称为平面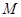 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:①设
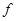 是平面
是平面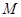 上的线性变换,
上的线性变换,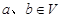 ,则
,则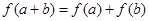 ;
;②若
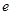 是平面
是平面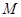 上的单位向量,对
上的单位向量,对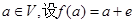 ,则
,则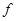 是平面
是平面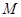 上的线性变换;
上的线性变换; ③对
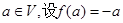 ,则
,则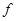 是平面
是平面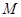 上的线性变换;
上的线性变换; ④设
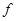 是平面
是平面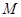 上的线性变换,
上的线性变换,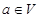 ,则对任意实数
,则对任意实数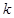 均有
均有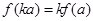 。
。其中的真命题是 .(写出所有真命题的编号)
①③④
试题分析:①在
 中,令
中,令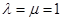 得:
得: ;故正确.
;故正确.②因为
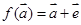 ,所以
,所以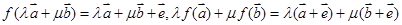 ,二者不相等,故不是线性变换.
,二者不相等,故不是线性变换.③因为
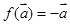 ,所以
,所以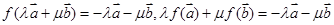 ,二者相等,故是线性变换.
,二者相等,故是线性变换.④在
 中,令
中,令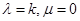 得:
得: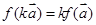 ;故正确.
;故正确.
练习册系列答案
相关题目
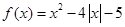 .
.
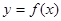 的图象;
的图象;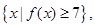 求集合A;
求集合A;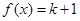 有两解,求实数
有两解,求实数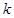 的取值范围.
的取值范围.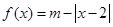 ,
, ,且
,且 的解集为
的解集为 .
. 的值;
的值; ,且
,且 ,求证:
,求证:
 ,
, ,且满足
,且满足 则
则
 的零点所在的区间为( )
的零点所在的区间为( )



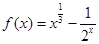 的零点所在区间是( )
的零点所在区间是( )



 ,若关于
,若关于 的方程
的方程 有3个不同的实根
有3个不同的实根 ,则
,则 等于( )
等于( )

 有唯一零点,则实数
有唯一零点,则实数 的取值范围是______.
的取值范围是______. ,则
,则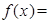 .
.