题目内容
正项数列{an}满足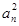 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an;
(2)令bn=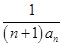 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
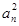 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.(1)求数列{an}的通项公式an;
(2)令bn=
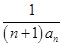 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.(1) an=2n (2) Tn=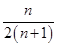
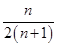
解:(1)已知an与n的关系式,求an,这一类题目应把式子进行变形,得an=f(n),从而求出通项公式.
由
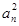 -(2n-1)an-2n=0,
-(2n-1)an-2n=0,得(an-2n)(an+1)=0.
故an=-1(因数列为正项数列,舍去)或an=2n.
(2)因bn=
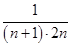 =
=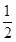 (
(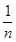 -
-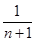 ),
),所以Tn=b1+b2+b3+…+bn
=
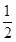 (
(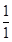 -
-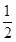 )+
)+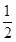 (
(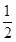 -
-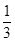 )+
)+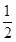 (
(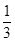 -
-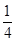 )+…+
)+…+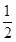 (
(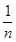 -
-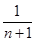 )
)=
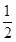 (
(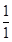 -
-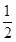 +
+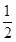 -
-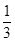 +
+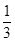 -
-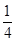 +…+
+…+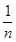 -
-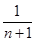 )
)=
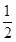 (1-
(1-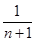 )
)=
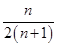 .
.
练习册系列答案
相关题目
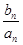 的最大值和最小值;
的最大值和最小值;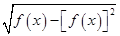 +
+ 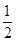 ,设an=[f(n)]2-f(n),数列{an}的前15项的和为
,设an=[f(n)]2-f(n),数列{an}的前15项的和为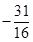 ,则f(15)= .
,则f(15)= .
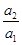 等于( )
等于( )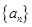 中,已知
中,已知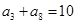 ,则
,则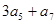 =( )
=( )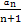 }的前n项和Sn等于 .
}的前n项和Sn等于 .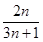 ,那么这个数列是( )
,那么这个数列是( )