题目内容
设曲线y=xn(1-x)在x=2处的切线与y轴交点的纵坐标为an,则数列{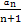
}的前n项和Sn等于 .
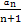}的前n项和Sn等于 .2n+1-2
∵y'=nxn-1-(n+1)xn,∴y'|x=2=n·2n-1-(n+1)·2n=-n·2n-1-2n,
∴切线方程为y+2n=(-n·2n-1-2n)(x-2),
令x=0得y=(n+1)·2n,即an=(n+1)·2n,
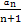∴=2n,∴Sn=2n+1-2.
∴切线方程为y+2n=(-n·2n-1-2n)(x-2),
令x=0得y=(n+1)·2n,即an=(n+1)·2n,
∴
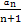=2n,∴Sn=2n+1-2.
练习册系列答案
相关题目
.
≤
+
+…+
<
.
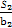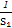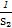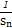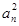-(2n-1)an-2n=0.
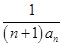,求数列{bn}的前n项和Tn.
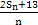,求数列{bn}的最小值项.