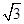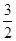题目内容
设P为椭圆
+
=1上的动点,则P到直线x+y-6=0的最小距离为( )
| x2 |
| 16 |
| y2 |
| 9 |
| A.1 | B.2 | C.
| D.
|
设直线x+y-C=0与椭圆
+
=1相切
联解消去x,得25y2-18Cy+9C2-144=0
∴△=(-18C)2-4×25×(9C2-144)=0,解之得C=5或-5
∴与直线x+y-6=0平行且与椭圆相切的直线方程为x+y±5=0
其中与直线x+y-6=0距离较近的是x+y-5=0,且距离为
=
,
∴P到直线x+y-6=0的最小距离为
,
故选C.
| x2 |
| 16 |
| y2 |
| 9 |
联解消去x,得25y2-18Cy+9C2-144=0
∴△=(-18C)2-4×25×(9C2-144)=0,解之得C=5或-5
∴与直线x+y-6=0平行且与椭圆相切的直线方程为x+y±5=0
其中与直线x+y-6=0距离较近的是x+y-5=0,且距离为
| 1 | ||
|
| ||
| 2 |
∴P到直线x+y-6=0的最小距离为
| ||
| 2 |
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
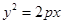 的焦点与双曲线
的焦点与双曲线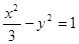 的右焦点重合,则
的右焦点重合,则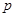 的值为( ).
的值为( ). 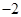
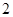
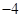
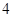
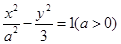 的离心率为2,则
的离心率为2,则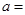
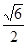
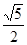
 的离心率为2,则
的离心率为2,则 等于( )
等于( )