题目内容

设椭圆
x2
a2
+
y2
b2
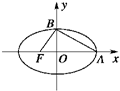
=1（a＞b＞0）的两个焦点是F1和F2，长轴是A1A2，P是椭圆上异于A1、A2的点，考虑如下四个命题：
①|PF1|-|A1F1|=|A1F2|-|PF2|；
②a-c＜|PF1|＜a+c；
③若b越接近于a，则离心率越接近于1；
④直线PA1与PA2的斜率之积等于-
b2
a2
．
其中正确的命题是（　　）
A．①②④B．①②③C．②③④D．①④
①由椭圆的定义和性质可得：|PF1|+|PF2|=2a，|A1F1|+|A1F2|=a-c+a+c=2a，
∴|A1F1|+|A1F2|=|PF1|+|PF2|，∴|PF1|-|A1F1|=|A1F2|-|PF2|，因此正确；
②∵|A1F1|＜|PF1|＜|AF2|，∴a-c＜|PF1|＜a+c，因此正确；
③由离心率计算公式e=
c
a
=
1-
b2
a2
可知：b越接近于a，则离心率越接近于0，因此③不正确；
④设P（x，y）（x≠±a），由
x2
a2
+
y2
b2
=1可得y2=b2(1-
x2
a2
)=
b2
a2
(a2-x2)，
则kPA1•kPA2=
y-0
x+a
•
y-0
x-a
=
y2
x2-a2
=
b2
a2
(a2-x2)
x2-a2
=-
b2
a2
，因此④正确．
综上可知：正确的是①、②、④．
故选：A．
练习册系列答案
相关题目
（文）椭圆具有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点．今有一个水平放置的椭圆形台球盘，点A、B是它的焦点，长轴长为2a，焦距为2c，静放在点A的小球（小球的半径忽略不计）从点A沿直线出发，经椭圆壁反射后第一次回到点A时，小球经过的路程是______．
椭圆
x2
36
+
y2
27
=1，过右焦点F作不垂直于x轴的弦交椭圆于A、B两点，AB的垂直平分线交x轴于N，则|NF|：|AB|等于______．
设F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，过F2的直线l与椭圆C相交于A，B两点，直线l的倾斜角为60°，F1到直线l的距离为2
3
．
（Ⅰ）求椭圆C的焦距；
（Ⅱ）如果
AF2
=2
F2B
，求椭圆C的方程．
已知两点A（-1，0），B（1，0），且点C（x，y）满足
(x-1)2+y2
|x-4|
=
1
2
，则|AC|+|BC|=（　　）
A．6B．2C．4D．不能确定
已知椭圆
x2
a2
+
y2
b2
=1上到点A（0，b）距离最远的点是B（0，-b），则椭圆的离心率的取值范围为（　　）
A．(0，
6
3
]		B．[
6
3
，1)		C．(0，
2
2
]		D．[
2
2
，1)
如图，椭圆中心在坐标原点，点F为左焦点，点B为短轴的上顶点，点A为长轴的右顶点．当
FB
⊥
BA
时，椭圆被称为“黄金椭圆”，则“黄金椭圆”的离心率e等于（　　）
A．
5
-1
2
B．
5
+1
4
C．
3
-1
2
D．
3
+1
4
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点是F1（-c，0）、F2（c，0），M是椭圆上一点，且
F1M
•
F2M
=0，则离心率e的取值范围是 ______．
设P为椭圆
x2
16
+
y2
9
=1上的动点，则P到直线x+y-6=0的最小距离为（　　）
A．1B．2C．
2
2
D．
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网