题目内容

已知椭圆的中心在原点，其中一个焦点为F1（
3
，0），且该焦点于长轴上较近的端点距离为2-
3
．
（1）示此椭圆的标准方程及离心率；
（2）设F2是椭圆另一个焦点，若P是该椭圆上一个动点，求
PF1
•
PF2
的取值范围．
（1）设所求的椭圆方程为
x2
a2
+
y2
b2
=1（a＞b＞0），
则
c=
3
3
a-c=2-
3
a2=b2+c2
解得a=2，b=1，c=
3

故所求椭圆的方程为
x2
4
+y2=1，离心率e=
c
a
=
3
2

（2）由（1）知F1（-
3
，0），设P（x，y），
则
PF1
•
PF2
=（-
3
-x，-y）•（
3
-x，-y）=x2+y2-3=
1
4
（3x2-8）
∵x∈[-2，2]，∴0≤x2≤4，
故
PF1
•
PF2
∈[-2，1]
练习册系列答案
相关题目
设F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，过F2的直线l与椭圆C相交于A，B两点，直线l的倾斜角为60°，F1到直线l的距离为2
3
．
（Ⅰ）求椭圆C的焦距；
（Ⅱ）如果
AF2
=2
F2B
，求椭圆C的方程．
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点是F1（-c，0）、F2（c，0），M是椭圆上一点，且
F1M
•
F2M
=0，则离心率e的取值范围是 ______．
“m=3”是“椭圆
x2
4
+
y2
m
=1焦距为2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件
已知F1，F2分别是椭圆的左，右焦点，现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M，N，若过F1的直线MF1是圆F2的切线，则椭圆的离心率为（　　）
A．
3
-1		B．2-
3
C．
2
2
D．
3
2
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为e=
2
2
，左、右焦点分别为F1、F2，点P的坐标为（2，
3
），且F2在线段PF1的中垂线上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）如果圆E：（x-
1
2
）2+y2=r2被椭圆C所覆盖，求圆的半径r的最大值．
设P为椭圆
x2
16
+
y2
9
=1上的动点，则P到直线x+y-6=0的最小距离为（　　）
A．1B．2C．
2
2
D．
2
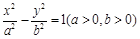已知F1、F2分别是双曲线的左、右焦点，点P为双曲线右支上的一点，满足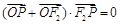（O为坐标原点），且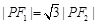，则该双曲线离心率为             ．
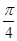已知双曲线的中心在原点，焦点在x轴上，它的一条渐近线与x轴的夹角为α，且<α<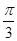，则双曲线的离心率的取值范围是________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网