题目内容
若函数y=f(x)(x∈R)满足f(x+1)=f(x-1),且x∈[-1,1]时,f(x)=1-x2,函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为( )| A.6 | B.7 | C.8 | D.9, |
C
因为函数y=f(x)(x∈R)满足f(x+1)=f(x-1),所以函数y=f(x)(x∈R)是周期为2的周期函数,又因为x∈[-1,1]时,f(x)=1-x2,所以作出函数f(x)(x∈R)和g(x)的图像,如图所示.
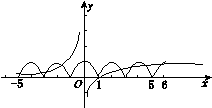
由图知函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为8.

由图知函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数为8.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
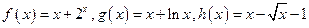 的零点分别为
的零点分别为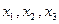 ,则
,则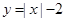 的图像与曲线
的图像与曲线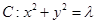 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数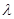 的取值范围是( )
的取值范围是( )



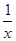 ,试求函数的零点个数.
,试求函数的零点个数.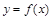 的定义域为D,如果存在区间
的定义域为D,如果存在区间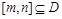 同时满足下列条件:
同时满足下列条件: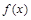 在[m,n]是单调的;②当定义域为[m,n]时,
在[m,n]是单调的;②当定义域为[m,n]时, 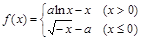 存在“H区间”,则正数
存在“H区间”,则正数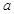 的取值范围是____________.
的取值范围是____________.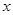 的方程
的方程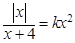 有四个不同的实数解,则实数k的取值范围是 .
有四个不同的实数解,则实数k的取值范围是 .