题目内容
【题目】已知椭圆
的左焦点为F，点
，过M的直线与椭圆E交于A，B两点，线段AB中点为C，设椭圆E在A，B两点处的切线相交于点P，O为坐标原点．
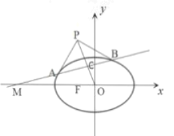
（1）证明：O、C、P三点共线；
（2）已知
是抛物线
的弦，所在直线过该抛物线的准线与y轴的交点，
是弦在两端点处的切线的交点，小明同学猜想：在定直线上．你认为小明猜想合理吗？若合理，请写出所在直线方程；若不合理，请说明理由．
【答案】（1）证明见解析； （2）合理，
在直线
上
【解析】
（1）设出直线
的方程，联立椭圆方程，根据韦达定理，利用导数求得任一点处切线的斜率，从而解得切线方程
，得到点
的坐标，由
即可容易判断；
（2）联立
的方程和抛物线方程，利用导数求得
处的切线方程，结合已知条件，即可容易证明.
（1）设
，
，直线AB的方程为
．
联立
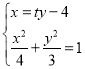，消去x整理得
，
由
﹐得
或
，
由椭圆对称性，设
是椭圆
在x轴上方的任意一点，
则由
，
得
﹐
所以在
处的切线斜率为
，
故在处切线方程为
，
结合
化简得
切线PA方程为：
，同理
，
联立两切线方程消去y得
，
联立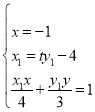
解得
，
由AB中点
及
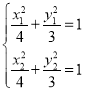可得
，
、C、P三点共线．
（2）合理，在直线上．
证明如下：设
，
，
直线
斜率一定存在，
联立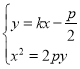
消去y得
，
，
由
得
，
．
抛物线在处的切线方程为
，
同理在处的切线方程为
联立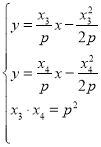
解得，
故在直线上．
练习册系列答案
相关题目
