题目内容
【题目】定义R在上的函数![]() 为奇函数,并且其图象关于x=1对称;当x∈(0,1]时,f(x)=9x﹣3.若数列{an}满足an=f(log2(64+n))(n∈N+);若n≤50时,当Sn=a1+a2+…+an取的最大值时,n=_____.
为奇函数,并且其图象关于x=1对称;当x∈(0,1]时,f(x)=9x﹣3.若数列{an}满足an=f(log2(64+n))(n∈N+);若n≤50时,当Sn=a1+a2+…+an取的最大值时,n=_____.
【答案】26
【解析】
先由函数![]() 的奇偶性和对称性求得函数的周期,再根据函数的值域及对数运算求得
的奇偶性和对称性求得函数的周期,再根据函数的值域及对数运算求得![]() 及
及![]() 时
时![]() 的取值范围,即可求得
的取值范围,即可求得![]() 取得最大值时
取得最大值时![]() 的值.
的值.
因为函数![]() 为奇函数,所以
为奇函数,所以![]() ,
,
又因为其图象关于直线x=1对称,
所以![]() ,即
,即![]() ,
,
所以![]() ,可得
,可得![]()
即函数f(x)是周期为4的周期函数,
因为当x∈(0,1]时,f(x)=9x﹣3,
所以![]() ,
,
因为函数![]() 为
为![]() 上的增函数,
上的增函数,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
作出函数![]() 在
在![]() 上的图象如图所示:
上的图象如图所示:
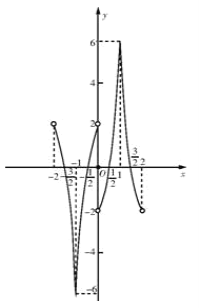
所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
由周期性可得:x∈(6,![]() )时,f(x)>0.
)时,f(x)>0.
x∈(![]() ,
,![]() )时,f(x)<0.
)时,f(x)<0.
f(![]() )=f(
)=f(![]() )=0.
)=0.
因为![]() ,
,
所以6<log2(64+n)<log2114<7.
而当6<log2(64+n)![]() 时,an>0
时,an>0
即当64<64+n<64![]() 90.496,an>0
90.496,an>0
∴n≤26时,an>0.
当27≤n≤50时,![]() log2(64+n)<log2114<7,此时an<0,
log2(64+n)<log2114<7,此时an<0,
∴当n=26时,Sn=a1+a2+…+an取的最大值.
故答案为:![]()

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】已知函数![]()
![]() ,g(x)=x2﹣1.
,g(x)=x2﹣1.
(1)求f(x)在点(0,f(0))处的切线方程.
(2)若h(x)=f(x)+g(x)有两个极值点x1,x2(x1<x2),求证:x1f(x1)>x2f(x2).
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题. 该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取![]() 件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
表1 甲流水线样本的频数分布表
质量指标值 | 频数 |
|
|
|
|
|
|
|
|
|
|
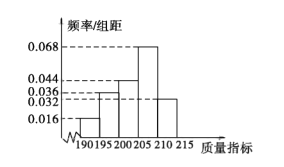
(1)若将频率视为概率,某个月内甲、乙两条流水线均生产了![]() 万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(2)在甲流水线抽取的样本的不合格品中随机抽取两件,求两件不合格品的质量指标值均偏大的概率;
(3)根据已知条件完成下面![]() 列联表,并判断在犯错误概率不超过
列联表,并判断在犯错误概率不超过![]() 的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

