Question

【题目】已知函数，g（x）＝x2﹣1．

（1）求f（x）在点（0，f（0））处的切线方程．

（2）若h（x）＝f（x）+g（x）有两个极值点x1，x2（x1＜x2），求证：x1f（x1）＞x2f（x2）．

Answer 1

【答案】（1）y＝﹣ax；（2）见解析

【解析】

对函数进行求导,利用导数的几何意义求出即为所求切线的斜率,代入点斜式求解即可;

对函数求导,根据题意知,为方程的两个不同的实根,利用判别式求出的取值范围,再利用韦达定理判断出的范围, 要证明x1f（x1）＞x2f（x2），即证明,根据题意分别求出的表达式,然后作差,结合韦达定理把用代换,构造函数m（x）＝2x﹣1+2（1﹣x）lnx﹣2xln（1﹣x），x,通过求导判断其单调性和最值,证明在上恒成立即可.

（1）由题意知,，f（0）＝0,，

故f（x）在（0，f（0））处的切线方程y＝﹣ax；

（2）由题意可知,h（x）＝aln（1﹣x）+x2﹣1，x＜1，

所以0在上有2个不同的实数根，

即方程﹣2x2+2x﹣a＝0在上有2个不同实根x1，x2，

所以△＝4﹣8a＞0，即0＜a，

由韦达定理可得,，∴，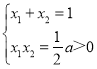

所以要证明x1f（x1）＞x2f（x2），即证明，

∵，

因为,

所以

＝2x1ln（1﹣x1）﹣（1+x1），

同理2x2ln（1﹣x2）﹣（1+x2），

所以2x1ln（1﹣x1）﹣（1+x1）﹣2x2ln（1﹣x2）+（1+x2）

＝2x1ln（1﹣x1）﹣2x2ln（1﹣x2）+x2﹣x1，

因为,所以

令m（x）＝2x﹣1+2（1﹣x）lnx﹣2xln（1﹣x），x，

∴2[ln（1﹣x）]

0在（）上恒成立，

故函数m（x）在（）上单调递增，m（x）＞m（）＝0，

故0，

即x1f（x1）＞x2f（x2）．