题目内容
【题目】如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
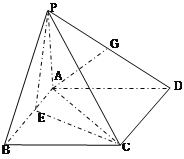
(1)求证:AG∥平面PEC;
(2)求AE的长;
(3)求二面角E—PC—A的正弦值.
【答案】(1)见解析.(2)![]() (3)
(3)![]() .
.
【解析】
试题解(1)证明:∵CD⊥AD,CD⊥PA
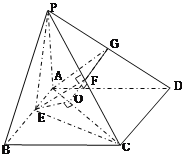
∴CD⊥平面PAD ∴CD⊥AG,
又PD⊥AG
∴AG⊥平面PCD
作EF⊥PC于F,因面PEC⊥面PCD
∴EF⊥平面PCD,
∴EF∥AG
又AG![]() 面PEC,EF
面PEC,EF![]() 面PEC,
面PEC,
∴AG∥平面PEC
(2)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD,
∴AE∥平面PCD.
∴AE∥GF.
∴四边形AEFG为平行四边形,∴AE=GF.
∵PA=3,AB=4,∴PD=5,AG=![]() ,
,
又PA2=PGPD,∴PG![]()
又![]() ,∴
,∴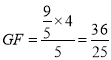 ,∴
,∴![]()
(3)过E作EO⊥AC于点O,易知EO⊥平面PAC,
又EF⊥PC,∴OF⊥PC∴∠EFO即为二面角E—PC—A的平面角
![]() ,
,
又EF=AG![]()
∴![]()

练习册系列答案
相关题目