题目内容
【题目】椭圆![]() 的顶点为
的顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点A且斜率为
,过点A且斜率为![]() 的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点
的直线与y轴交于点P,与椭圆交于另一个点B,且点B在x轴上的射影恰好为点![]() .
.
(1)求椭圆C的标准方程;
(2)M为椭圆C上一动点,![]() 是椭圆C长轴上的一个点,直线MQ与椭圆C的另一个交点为N,令
是椭圆C长轴上的一个点,直线MQ与椭圆C的另一个交点为N,令![]() ,若t值与点M的位置无关,则称此时的点Q为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
,若t值与点M的位置无关,则称此时的点Q为“稳定点”,试求出所有“稳定点”,若没有,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]()
【解析】
(1)由题意可得![]() ,直线
,直线![]() ,联立即可求出
,联立即可求出![]() ,再求出
,再求出![]() 即可得解;
即可得解;
(2)当直线斜率不为0时,设直线MQ![]() ,
,![]() ,
,![]() ,联立方程得
,联立方程得![]() ,
,![]() ,转化条件
,转化条件![]() ,
,![]() ,则
,则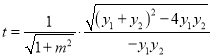 ,化简即可得解,再验证对于
,化简即可得解,再验证对于![]() 依然成立即可.
依然成立即可.
(1)![]() 点B在x轴上的射影恰好为点
点B在x轴上的射影恰好为点![]() ,椭圆顶点为
,椭圆顶点为![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,直线
,直线![]() ,
,
![]()
![]() 解得
解得![]() 或
或![]() (舍去),
(舍去),![]()
![]() .
.
![]() 椭圆C的标准方程为
椭圆C的标准方程为![]() .
.
(2)当直线斜率不为0时,设直线MQ![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,
,
则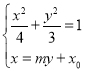 ,消去
,消去![]() 得
得![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
由弦长公式得![]() ,
,![]() ,
,
![]()
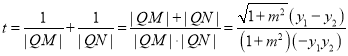
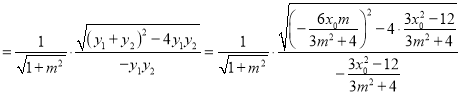
![]()
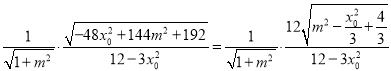 ,
,
![]() 当
当![]() 即
即![]() 时,
时,![]() 为定值
为定值![]() .
.
又 当![]() ,直线MQ方程为
,直线MQ方程为![]() 时,
时,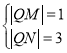 或
或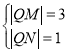 ,
,![]() .
.
![]() 该椭圆稳定点为
该椭圆稳定点为![]() 和
和![]() .
.

练习册系列答案
相关题目