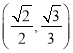题目内容
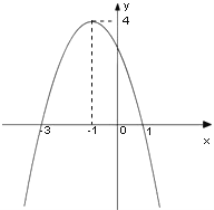
【题目】如图是一个二次函数y=f(x)的图象
(1)写出这个二次函数的零点
(2)求这个二次函数的解析式
(3)当实数k在何范围内变化时,函数g(x)=f(x)-kx在区间[-2,2]上是单调函数?
【答案】(1)零点是-3,1(2)y=-x2-2x+3 (3)k≤-6或k≥2时,g(x)在[-2,2]上是单调函数
【解析】
(1)根据图象,找函数图象与横轴交点的横坐标即可求得函数的零点;(2)由顶点是![]() 可设函数为
可设函数为![]() ,再代入
,再代入![]() 即可求得函数的解析式;(3)先化简函数
即可求得函数的解析式;(3)先化简函数![]()
![]() 易知图象开口向下,对称轴为
易知图象开口向下,对称轴为![]() ,因为是单调函数,利用对称轴在区间的两侧列不等式求解即可.
,因为是单调函数,利用对称轴在区间的两侧列不等式求解即可.
(1)由图可知,此二次函数的零点是-3,1
(2)∵顶点是(-1,4)
∴设函数为:y=a(x+1)2+4,
∵(-3,0)在图象上
∴a=-1
∴函数为y=-x2-2x+3
(3)∵g(x)=-x2-2x+3-kx=-x2-(k+2)x+3
∴图象开口向下,对称轴为![]()
当![]() ,即k≥2时,g(x)在[-2,2]上是减函数
,即k≥2时,g(x)在[-2,2]上是减函数
当![]() ,即k≤-6时,g(x)在[-2,2]上是增函数
,即k≤-6时,g(x)在[-2,2]上是增函数
综上所述k≤-6或k≥2时,g(x)在[-2,2]上是单调函数

练习册系列答案
相关题目