题目内容
【题目】已知三点O（0，0），A（﹣2，1），B（2，1），曲线C上任意一点M（x，y）满足| 
+ 
|= 
（ 
+ 
）+2．
（1）求曲线C的方程；
（2）动点Q（x0 ， y0）（﹣2＜x0＜2）在曲线C上，曲线C在点Q处的切线为直线l：是否存在定点P（0，t）（t＜0），使得l与PA，PB都相交，交点分别为D，E，且△QAB与△PDE的面积之比是常数？若存在，求t的值．若不存在，说明理由．
【答案】
（1）解：由 
=（﹣2﹣x，1﹣y）， 
=（2﹣x，1﹣y）可得 + =（﹣2x，2﹣2y），
∴| + |= 
， 
（ 
+ 
）+2=（x，y）（0，2）+2=2y+2．
由题意可得 =2y+2，化简可得 x2=4y．
（2）解：假设存在点P（0，t）（t＜0），满足条件，则直线PA的方程是y= 
，直线PB的方程是y= 
∵﹣2＜x0＜2，∴ 
①当﹣1＜t＜0时， 
，存在x0∈（﹣2，2），使得 
∴l∥PA，∴当﹣1＜t＜0时，不符合题意；
②当t≤﹣1时， 
， 
，
∴l与直线PA，PB一定相交，分别联立方程组
， 
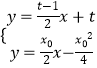，解得D，E的横坐标分别是 
， 
∴ 
∵|FP|=﹣ 
∴ 
= 
∵ 
∴ 
× 
∵x0∈（﹣2，2），△QAB与△PDE的面积之比是常数
∴ 
，解得t=﹣1，
∴△QAB与△PDE的面积之比是2．
【解析】（1）用坐标表示 ， ，从而可得 + ，可求| + |，利用向量的数量积，结合M（x，y）满足| + |= （ + ）+2，可得曲线C的方程；（2）假设存在点P（0，t）（t＜0），满足条件，则直线PA的方程是y= ，直线PB的方程是y= 分类讨论：①当﹣1＜t＜0时，l∥PA，不符合题意；②当t≤﹣1时， ， ，分别联立方程组，解得D，E的横坐标，进而可得△QAB与△PDE的面积之比，利用其为常数，即可求得结论．
快捷英语周周练系列答案
