题目内容
已知函数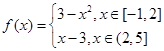 .
.
(1)在如图给定的直角坐标系内画出 的图像;
的图像;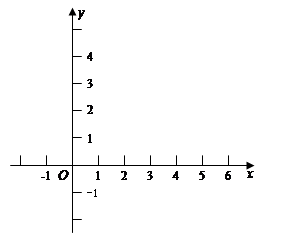
(2)写出 的单调递增区间及值域;
的单调递增区间及值域;
(3)求不等式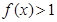 的解集.
的解集.
(1)见解析
(2) 的单调递增区间
的单调递增区间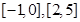 , 值域为
, 值域为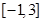 ;
;
(3)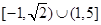
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知函数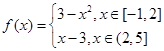 .
.
(1)在如图给定的直角坐标系内画出 的图像;
的图像;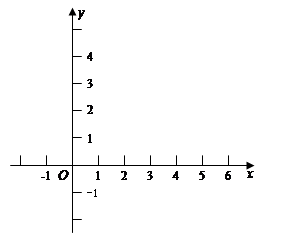
(2)写出 的单调递增区间及值域;
的单调递增区间及值域;
(3)求不等式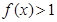 的解集.
的解集.
(1)见解析
(2) 的单调递增区间
的单调递增区间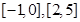 , 值域为
, 值域为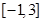 ;
;
(3)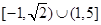
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案