题目内容
已知圆M过定点 且圆心M在抛物线
且圆心M在抛物线 上运动,若y轴截圆M所得的弦长为AB,则弦长
上运动,若y轴截圆M所得的弦长为AB,则弦长 等于
等于
| A.4 | B.3 |
| C.2 | D.与点M位置有关的值 |
A
解析试题分析:设圆心坐标为(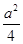 ,a),由于过定点(2,1),则其半径为
,a),由于过定点(2,1),则其半径为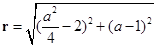 ,那么可知其圆的方程为
,那么可知其圆的方程为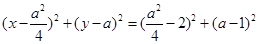 ,令x=0,可得关于x的一元二次方程,结合韦达定理可知弦长为
,令x=0,可得关于x的一元二次方程,结合韦达定理可知弦长为 =4,故选A.
=4,故选A.
考点:直线与圆锥曲线的综合应用
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.属于中档题。

练习册系列答案
相关题目
已知直线 与圆
与圆 相切,若对任意的
相切,若对任意的 均有不等式
均有不等式 成立,那么正整数
成立,那么正整数 的最大值是( )
的最大值是( )
| A.3 | B.5 | C.7 | D.9 |
已知两点 到直线
到直线 的距离分别为
的距离分别为 ,则满足条件的直线
,则满足条件的直线 共有( )条
共有( )条
| A.1 | B.2 | C.3 | D.4 |
如果圆x2+y2+Dx+Ey+F=0与x轴切于原点, 那么( )
| A.D=0,E≠0, F≠0 | B.E=F=0,D≠0 | C.D="F=0," E≠0 | D.D=E=0,F≠0 |
若过定点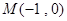 且斜率为
且斜率为 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则 的取值范围是( ).
的取值范围是( ).
A. | B.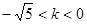 |
C. | D. |
以点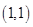 和
和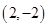 为直径两端点的圆的方程是( )
为直径两端点的圆的方程是( )
A.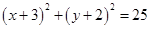 | B.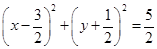 |
C.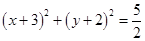 | D. |
已知圆 :
: ,过
,过 轴上的点
轴上的点 存在圆
存在圆 的割线
的割线 ,使得
,使得 ,则点
,则点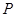 的横坐标
的横坐标 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若直线 与圆
与圆 有公共点,则实数
有公共点,则实数 取值范围是( )
取值范围是( )
A. | B. |
C. | D. |
若方程 表示一个圆,则有( )
表示一个圆,则有( )
A. | B.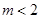 | C. | D. |