题目内容
已知圆 :
: ,过
,过 轴上的点
轴上的点 存在圆
存在圆 的割线
的割线 ,使得
,使得 ,则点
,则点 的横坐标
的横坐标 的取值范围是( )
的取值范围是( )
A. | B.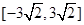 | C. | D.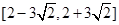 |
C
解析试题分析:极端原理,或利用圆幂定理和切长定理
设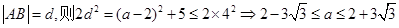 ,故可知点P的横坐标
,故可知点P的横坐标 的取值范围是
的取值范围是 ,选C.
,选C.
考点:直线与圆的位置关系
点评:解决的关键是利用切线长定理,以及圆内性质的综合运用,属于基础题。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
若直线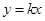 与圆
与圆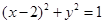 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则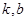 的值分别为
的值分别为
A.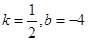 | B.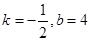 |
C.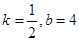 | D.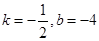 |
圆(x-3)2+(y+4)2=1关于直线y=—x+6对称的圆的方程是 ( )
| A.(x+10)2+(y+3)2=1 | B.(x-10)2+(y-3)2=1 |
| C.(x-3)2+(y+10)2=1 | D.(x-3)2+(y-10)2=1 |
已知圆M过定点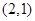 且圆心M在抛物线
且圆心M在抛物线 上运动,若y轴截圆M所得的弦长为AB,则弦长
上运动,若y轴截圆M所得的弦长为AB,则弦长 等于
等于
| A.4 | B.3 |
| C.2 | D.与点M位置有关的值 |
圆 ,圆
,圆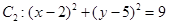 ,则这两圆公切线的条数
,则这两圆公切线的条数
为 ( )
| A.1 | B.2 | C.3 | D.4 |
圆C1:(x-2)2+(y+2)2=9与圆C2:(x+1)2+(y-2)2=4的公切线有( )
| A.0条 | B.2条 | C.3条 | D.4条 |
方程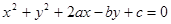 表示圆心为C(2,2),半径为2的圆,则
表示圆心为C(2,2),半径为2的圆,则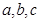 的值依次为 ( )
的值依次为 ( )
| A.2、4、4; | B.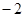 、4、4; 、4、4; | C.2、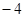 、4; 、4; | D.2、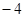 、 、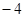 |
已知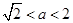 ,则函数
,则函数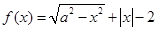 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
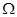 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、 ,则称P优于
,则称P优于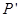 ,如果
,如果