题目内容
已知直线
与圆
相切，若对任意的
均有不等式
成立，那么正整数
的最大值是（ ）
| A．3 | B．5 | C．7 | D．9 |
A
解析试题分析：∵直线
与圆相切，∴
，即
（※），令t=2m+n，则n=t-2m，代入（※）化简得
，由题意该式有解，∴其判别式
，解得t≥3，故正整数的最大值是3，故选A
考点：本题考查了直线与圆的位置关系
点评：研究直线和圆的位置关系的相关问题时通常采用“几何法”即抓住圆心到直线的的距离与半径的关系
练习册系列答案
相关题目
已知圆C与直线
及
都相切，圆心在直线
上，则圆C的方程为（ ）
A． | B． |
C． | D． |
已知圆心为
的圆，经过点
，则该圆的标准方程是
A． |
B． |
C． |
D． |
过点
与圆
相交的所有直线中，被圆截得的弦最长的直线方程是（ ）
A． | B． | C． | D． |
以极坐标系中的点
为圆心，
为半径的圆的直角坐标方程是( )
A． | B． | C． | D． |
设直线
与圆
相交于
点，则弦
的长等于( )
A． | B． | C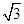． | D．1 |
若直线
与圆
的两个交点关于直线
对称，则
的值分别为
A． | B． |
C． | D． |
若圆C：(x＋1)2＋(y－1)2＝8上有且只有两个点到直线x＋y＋m＝0的距离等于
，则实数m的取值范围是( )．
| A．(－8，－4)∪(4,8) | B．(－6，－2)∪(2,6) |
| C．(2,6) | D．(4,8) |
已知圆M过定点
且圆心M在抛物线
上运动，若y轴截圆M所得的弦长为AB，则弦长
等于
| A．4 | B．3 |
| C．2 | D．与点M位置有关的值 |