题目内容
已知两点 到直线
到直线 的距离分别为
的距离分别为 ,则满足条件的直线
,则满足条件的直线 共有( )条
共有( )条
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:由A和B的坐标,利用两点间的距离公式求出|AB|的长,然后以A为圆心, 为半径画圆A,以B为圆心
为半径画圆A,以B为圆心 为半径画圆B,由d=R+r,得到两圆外切,可得出公切线有3条,即可得到满足题意的直线l共有3条。
为半径画圆B,由d=R+r,得到两圆外切,可得出公切线有3条,即可得到满足题意的直线l共有3条。
解:∵A(1,2),B(3,1),∴|AB|= ,分别以A,B为圆心,
,分别以A,B为圆心, ,
, 为半径作两个圆,如图所示:
为半径作两个圆,如图所示:
即d=R+r,∴两圆外切,有三条共切线,则满足条件的直线l共有3条.故选C
考点:圆与圆位置关系的判定
点评:此题考查了圆与圆位置关系的判定,以及直线与圆的位置关系,圆与圆位置关系由R,r及d间的关系来判定,当d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R-r时,两圆外离,解题的关键是根据题意画出相应的图形,找出两圆的公切线的条数即为所求直线l的条数

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知圆心为 的圆,经过点
的圆,经过点 ,则该圆的标准方程是
,则该圆的标准方程是
A. |
B. |
C. |
D. |
若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 的值分别为
的值分别为
A. | B. |
C. | D. |
若圆C:(x+1)2+(y-1)2=8上有且只有两个点到直线x+y+m=0的距离等于 ,则实数m的取值范围是( ).
,则实数m的取值范围是( ).
| A.(-8,-4)∪(4,8) | B.(-6,-2)∪(2,6) |
| C.(2,6) | D.(4,8) |
两圆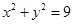 和
和 的位置关系是( )
的位置关系是( )
| A.相离 | B.相交 | C.内切 | D.外切 |
若实数x,y满足x²+y²-2x+4y=0,则x-2y的最大值为 ( )
A. | B.10 | C.9 | D.5+2 |
圆(x-3)2+(y+4)2=1关于直线y=—x+6对称的圆的方程是 ( )
| A.(x+10)2+(y+3)2=1 | B.(x-10)2+(y-3)2=1 |
| C.(x-3)2+(y+10)2=1 | D.(x-3)2+(y-10)2=1 |
已知圆M过定点 且圆心M在抛物线
且圆心M在抛物线 上运动,若y轴截圆M所得的弦长为AB,则弦长
上运动,若y轴截圆M所得的弦长为AB,则弦长 等于
等于
| A.4 | B.3 |
| C.2 | D.与点M位置有关的值 |
方程 表示圆心为C(2,2),半径为2的圆,则
表示圆心为C(2,2),半径为2的圆,则 的值依次为 ( )
的值依次为 ( )
| A.2、4、4; | B. 、4、4; 、4、4; | C.2、 、4; 、4; | D.2、 、 、 |