题目内容
(本小题满分14分)
已知双曲线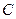 :
: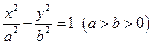 和圆
和圆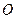 :
: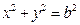 (其中原点
(其中原点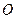 为圆心),过双曲线
为圆心),过双曲线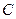 上一点
上一点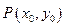 引圆
引圆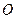 的两条切线,切点分别为
的两条切线,切点分别为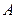 、
、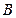 .
.
(1)若双曲线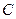 上存在点
上存在点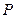 ,使得
,使得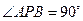 ,求双曲线离心率
,求双曲线离心率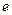 的取值范围;
的取值范围;
(2)求直线 的方程;
的方程;
(3)求三角形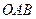 面积的最大值.
面积的最大值.
已知双曲线
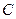 :
: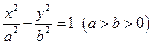 和圆
和圆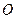 :
: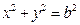 (其中原点
(其中原点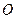 为圆心),过双曲线
为圆心),过双曲线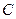 上一点
上一点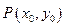 引圆
引圆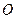 的两条切线,切点分别为
的两条切线,切点分别为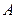 、
、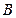 .
.(1)若双曲线
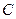 上存在点
上存在点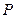 ,使得
,使得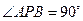 ,求双曲线离心率
,求双曲线离心率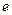 的取值范围;
的取值范围;(2)求直线
 的方程;
的方程;(3)求三角形
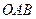 面积的最大值.
面积的最大值.(本小题主要考查圆、双曲线、直线方程和不等式等基础知识,考查运算求解能力和推理论证能力,以及数形结合、分类讨论思想和创新意识等.)
解:(1)因为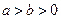 ,所以
,所以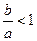 ,所以
,所以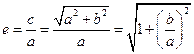
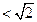 .…………………1分
.…………………1分
由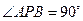 及圆的性质,可知四边形
及圆的性质,可知四边形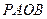 是正方形,所以
是正方形,所以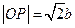 .
.
因为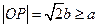 ,所以
,所以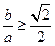 ,所以
,所以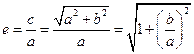
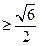 .……………3分
.……………3分
故双曲线离心率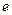 的取值范围为
的取值范围为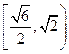 .…………………………………………………………4分
.…………………………………………………………4分
(2)方法1:因为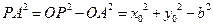 ,
,
所以以点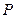 为圆心,
为圆心,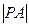 为半径的圆
为半径的圆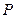 的方程为
的方程为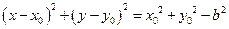 .………5分
.………5分
因为圆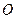 与圆
与圆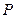 两圆的公共弦所在的直线即为直线
两圆的公共弦所在的直线即为直线 ,……………………………………………6分
,……………………………………………6分
所以联立方程组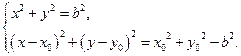 ………………………………………………7分
………………………………………………7分
消去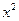 ,
,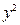 ,即得直线
,即得直线 的方程为
的方程为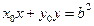 .………………………………………………8分
.………………………………………………8分
方法2:设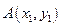
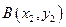 ,已知点
,已知点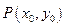 ,
,
则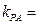
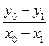 ,
,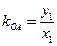
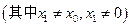 .
.
因为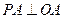 ,所以
,所以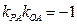 ,即
,即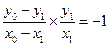 .…………………………………………5分
.…………………………………………5分
整理得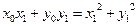 .
.
因为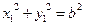 ,所以
,所以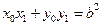 .……………………………………………………………6分
.……………………………………………………………6分
因为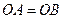 ,
,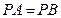 ,根据平面几何知识可知,
,根据平面几何知识可知,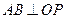 .
.
因为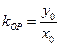 ,所以
,所以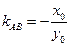 .………………………………………………………………………7分
.………………………………………………………………………7分
所以直线 方程为
方程为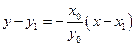 .
.
即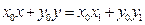 .
.
所以直线 的方程为
的方程为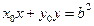 .………………………………………………………………8分
.………………………………………………………………8分
方法3:设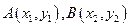 ,已知点
,已知点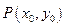 ,
,
则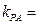
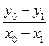 ,
,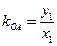
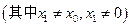 .
.
因为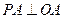 ,所以
,所以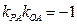 ,即
,即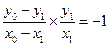 .…………………………………………5分
.…………………………………………5分
整理得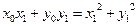 .
.
因为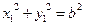 ,所以
,所以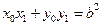 .……6分
.……6分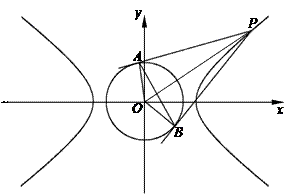
这说明点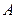 在直线
在直线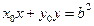 上.…………7分
上.…………7分
同理点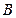 也在直线
也在直线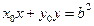 上.
上.
所以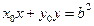 就是直线
就是直线 的方程.……8分
的方程.……8分
(3)由(2)知,直线 的方程为
的方程为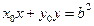 ,
,
所以点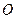 到直线
到直线 的距离为
的距离为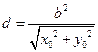 .
.
因为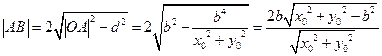 ,
,
所以三角形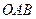 的面积
的面积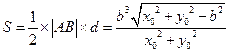 .……………………………………10分
.……………………………………10分
以下给出求三角形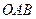 的面积
的面积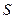 的三种方法:
的三种方法:
方法1:因为点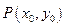 在双曲线
在双曲线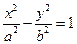 上,
上,
所以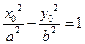 ,即
,即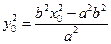
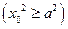 .
.
设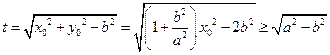 ,
,
所以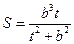 .………………………………………………………………………………………11分
.………………………………………………………………………………………11分
因为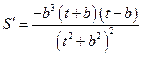 ,
,
所以当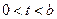 时,
时,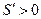 ,当
,当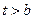 时,
时,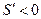 .
.
所以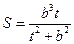 在
在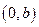 上单调递增,在
上单调递增,在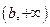 上单调递减.……………………………………12分
上单调递减.……………………………………12分
当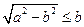 ,即
,即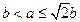 时,
时,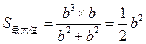 ,…………………………………13分
,…………………………………13分
当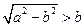 ,即
,即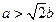 时,
时,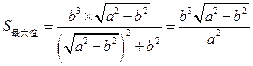 .
.
综上可知,当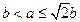 时,
时,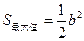 ;当
;当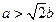 时,
时,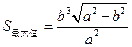 .………14分
.………14分
方法2:设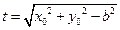 ,则
,则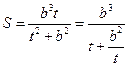 .…………………………………………11分
.…………………………………………11分
因为点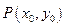 在双曲线
在双曲线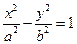 上,即
上,即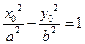 ,即
,即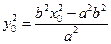
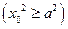 .
.
所以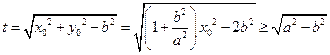 .
.
令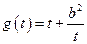 ,则
,则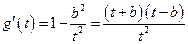 .
.
所以当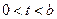 时,
时,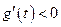 ,当
,当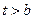 时,
时,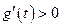 .
.
所以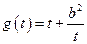 在
在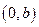 上单调递减,在
上单调递减,在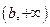 上单调递增.…………………………………12分
上单调递增.…………………………………12分
当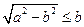 ,即
,即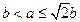 时,
时,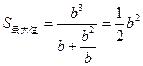 ,……………………………………13分
,……………………………………13分
当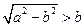 ,即
,即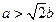 时,
时,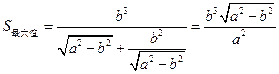 .
.
综上可知,当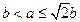 时,
时,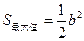 ;当
;当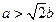 时,
时,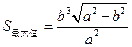 .………14分
.………14分
方法3:设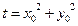 ,则
,则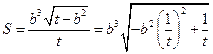 .…………………………………11分
.…………………………………11分
因为点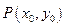 在双曲线
在双曲线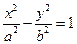 上,即
上,即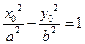 ,即
,即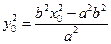
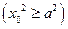 .
.
所以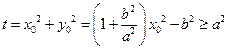 .
.
令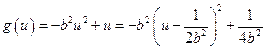 ,
,
所以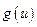 在
在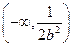 上单调递增,在
上单调递增,在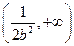 上单调递减.………………………………12分
上单调递减.………………………………12分
因为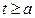 ,所以
,所以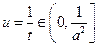 ,
,
当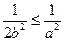 ,即
,即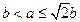 时,
时,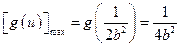 ,此时
,此时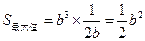 .
.
………………………………13分
当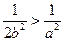 ,即
,即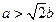 时,
时,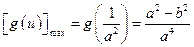 ,此时
,此时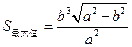 .
.
综上可知,当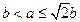 时,
时,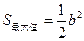 ;当
;当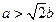 时,
时,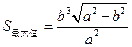 .………14分
.………14分
解:(1)因为
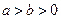 ,所以
,所以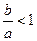 ,所以
,所以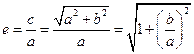
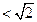 .…………………1分
.…………………1分由
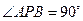 及圆的性质,可知四边形
及圆的性质,可知四边形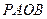 是正方形,所以
是正方形,所以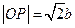 .
.因为
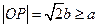 ,所以
,所以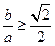 ,所以
,所以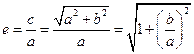
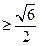 .……………3分
.……………3分故双曲线离心率
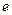 的取值范围为
的取值范围为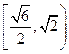 .…………………………………………………………4分
.…………………………………………………………4分(2)方法1:因为
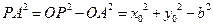 ,
,所以以点
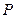 为圆心,
为圆心,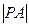 为半径的圆
为半径的圆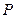 的方程为
的方程为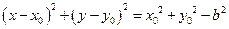 .………5分
.………5分因为圆
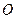 与圆
与圆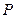 两圆的公共弦所在的直线即为直线
两圆的公共弦所在的直线即为直线 ,……………………………………………6分
,……………………………………………6分所以联立方程组
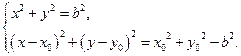 ………………………………………………7分
………………………………………………7分消去
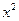 ,
,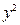 ,即得直线
,即得直线 的方程为
的方程为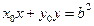 .………………………………………………8分
.………………………………………………8分方法2:设
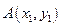
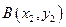 ,已知点
,已知点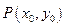 ,
,则
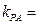
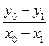 ,
,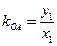
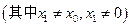 .
.因为
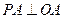 ,所以
,所以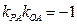 ,即
,即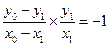 .…………………………………………5分
.…………………………………………5分整理得
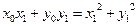 .
.因为
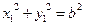 ,所以
,所以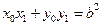 .……………………………………………………………6分
.……………………………………………………………6分因为
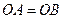 ,
,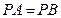 ,根据平面几何知识可知,
,根据平面几何知识可知,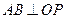 .
.因为
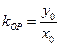 ,所以
,所以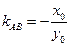 .………………………………………………………………………7分
.………………………………………………………………………7分所以直线
 方程为
方程为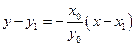 .
.即
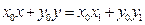 .
.所以直线
 的方程为
的方程为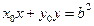 .………………………………………………………………8分
.………………………………………………………………8分方法3:设
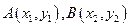 ,已知点
,已知点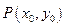 ,
,则
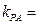
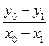 ,
,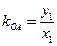
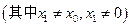 .
.因为
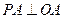 ,所以
,所以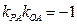 ,即
,即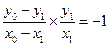 .…………………………………………5分
.…………………………………………5分整理得
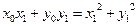 .
.因为
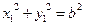 ,所以
,所以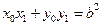 .……6分
.……6分
这说明点
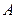 在直线
在直线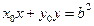 上.…………7分
上.…………7分同理点
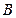 也在直线
也在直线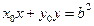 上.
上.所以
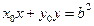 就是直线
就是直线 的方程.……8分
的方程.……8分(3)由(2)知,直线
 的方程为
的方程为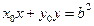 ,
,所以点
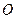 到直线
到直线 的距离为
的距离为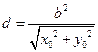 .
.因为
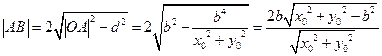 ,
,所以三角形
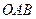 的面积
的面积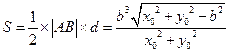 .……………………………………10分
.……………………………………10分以下给出求三角形
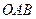 的面积
的面积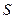 的三种方法:
的三种方法:方法1:因为点
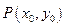 在双曲线
在双曲线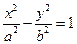 上,
上,所以
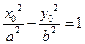 ,即
,即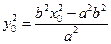
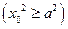 .
.设
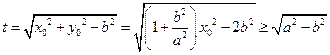 ,
,所以
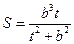 .………………………………………………………………………………………11分
.………………………………………………………………………………………11分因为
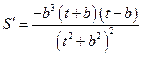 ,
,所以当
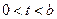 时,
时,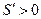 ,当
,当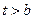 时,
时,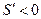 .
.所以
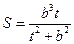 在
在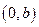 上单调递增,在
上单调递增,在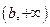 上单调递减.……………………………………12分
上单调递减.……………………………………12分当
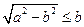 ,即
,即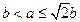 时,
时,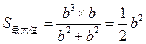 ,…………………………………13分
,…………………………………13分当
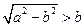 ,即
,即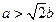 时,
时,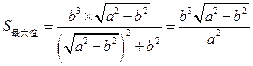 .
.综上可知,当
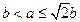 时,
时,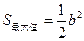 ;当
;当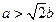 时,
时,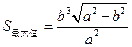 .………14分
.………14分方法2:设
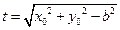 ,则
,则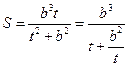 .…………………………………………11分
.…………………………………………11分因为点
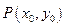 在双曲线
在双曲线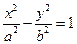 上,即
上,即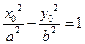 ,即
,即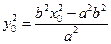
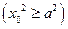 .
.所以
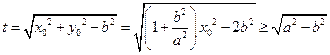 .
.令
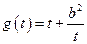 ,则
,则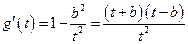 .
.所以当
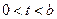 时,
时,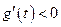 ,当
,当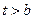 时,
时,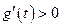 .
.所以
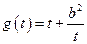 在
在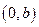 上单调递减,在
上单调递减,在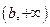 上单调递增.…………………………………12分
上单调递增.…………………………………12分当
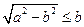 ,即
,即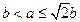 时,
时,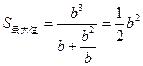 ,……………………………………13分
,……………………………………13分当
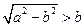 ,即
,即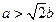 时,
时,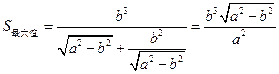 .
.综上可知,当
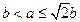 时,
时,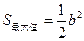 ;当
;当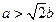 时,
时,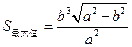 .………14分
.………14分方法3:设
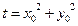 ,则
,则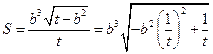 .…………………………………11分
.…………………………………11分因为点
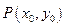 在双曲线
在双曲线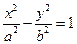 上,即
上,即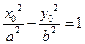 ,即
,即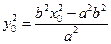
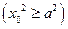 .
.所以
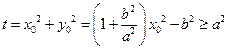 .
.令
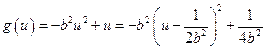 ,
,所以
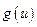 在
在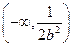 上单调递增,在
上单调递增,在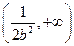 上单调递减.………………………………12分
上单调递减.………………………………12分因为
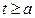 ,所以
,所以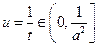 ,
,当
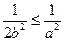 ,即
,即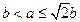 时,
时,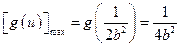 ,此时
,此时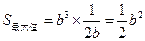 .
.………………………………13分
当
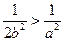 ,即
,即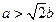 时,
时,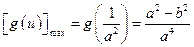 ,此时
,此时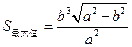 .
.综上可知,当
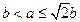 时,
时,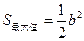 ;当
;当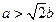 时,
时,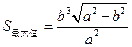 .………14分
.………14分略

练习册系列答案
相关题目
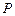 是椭圆
是椭圆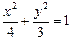 上一动点,点
上一动点,点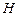 是点
是点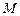 在
在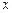 轴上的射影,坐标平面
轴上的射影,坐标平面 内动点
内动点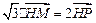 (
(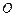 为坐标原点),设动点
为坐标原点),设动点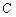 .
.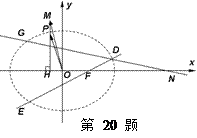
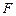 的直线
的直线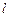 交曲线
交曲线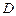 ,
,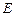 两点,且
两点,且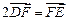 ,点
,点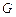 ,求直线
,求直线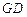 的方程.
的方程.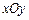 中,
中,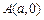
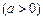 ,
,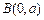 ,
,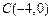 ,
, ,设
,设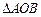 的外接圆圆心为E.
的外接圆圆心为E.
 (1)若⊙E与直线CD相切,求实数a的值;
(1)若⊙E与直线CD相切,求实数a的值;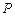 在圆
在圆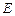 上,使
上,使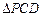 的面积等于12的点
的面积等于12的点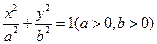 的右顶点为
的右顶点为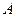 ,点
,点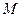 在椭圆上,且它的横坐标为1,点
在椭圆上,且它的横坐标为1,点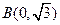 ,且
,且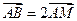 .
.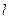 与椭圆交于另一点
与椭圆交于另一点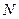 ,若线段
,若线段 的垂直平分线经过点
的垂直平分线经过点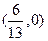 ,求直线
,求直线 中,已知动点
中,已知动点 到点
到点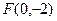 的距离为
的距离为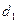 ,到
,到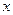 轴的距离为
轴的距离为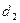 ,且
,且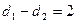 .
.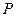 的轨迹
的轨迹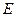 的方程;
的方程;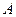 、
、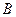 是(I)中
是(I)中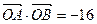 ,过
,过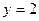 的垂线,垂足分别为
的垂线,垂足分别为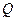 .证明:直线
.证明:直线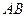 过定点
过定点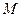 ,且
,且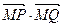 为定值.
为定值.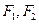 ,离心率为
,离心率为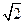 ,且过点
,且过点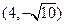 ,
,
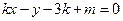 (其中
(其中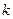 为参数)所过的定点
为参数)所过的定点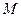 恰在双曲线上,求证:
恰在双曲线上,求证: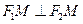 。
。 :“椭圆
:“椭圆 的焦点在x轴上” ,命题
的焦点在x轴上” ,命题 :只有一个实数
:只有一个实数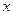 满足不等式
满足不等式 . 若命题“p且q”是真命题,求实数a的值
. 若命题“p且q”是真命题,求实数a的值 .
.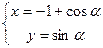
 上任意一点,则(x-2)2+(x+4)2的最大值是
上任意一点,则(x-2)2+(x+4)2的最大值是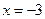 的距离小1,求点M满足的方程。
的距离小1,求点M满足的方程。