题目内容
【题目】某二手交易市场对某型号的二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数x | 2 | 4 | 6 | 8 | 10 |
销售价格y | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求y关于x的回归直线方程![]() .
.
(参考公式: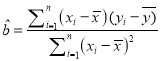 ,
,![]() )
)
(2)已知每辆该型号汽车的收购价格为ω=0.05x2﹣1.75x+17.2万元,根据(1)中所求的回归方程,预测x为何值时,销售一辆该型号汽车所获得的利润z最大?(利润=销售价格﹣收购价格)
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】
(1)先求样本中心![]() ,再求
,再求![]() ,最后将
,最后将![]() 代入
代入![]() 求
求![]() ,即可求解;
,即可求解;
(2)先列出利润的表达式z=﹣0.05x2+0.3x+1.5,再结合二次函数性质即可求解最值;
(1)由表中数据,计算![]() (2+4+6+8+10)=6,
(2+4+6+8+10)=6,
![]() (16+13+9.5+7+4.5)=10,
(16+13+9.5+7+4.5)=10,
![]() (xi
(xi![]() )(yi
)(yi![]() )=(﹣4)×6+(﹣2)×3+0×(﹣0.5)+2×(﹣3)+4×(﹣5.5)=﹣58.5;
)=(﹣4)×6+(﹣2)×3+0×(﹣0.5)+2×(﹣3)+4×(﹣5.5)=﹣58.5;
![]() (﹣4)2+(﹣2)2+02+22+42=40,
(﹣4)2+(﹣2)2+02+22+42=40,
由最小二乘法求得![]() 1.45,
1.45,
![]() 10﹣(﹣1.45)×6=18.7,
10﹣(﹣1.45)×6=18.7,
∴y关于x的回归直线方程为![]() ;
;
(2)根据题意利润函数为
z=(﹣1.45x+18.7)﹣(0.05x2﹣1.75x+17.2)=﹣0.05x2+0.3x+1.5,
∴当![]() 时,利润z取得最大值.
时,利润z取得最大值.

练习册系列答案
相关题目