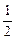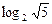题目内容
(Ⅰ)已知函数: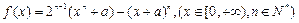 求函数
求函数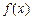 的最小值;
的最小值;
(Ⅱ)证明: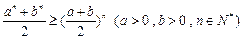 ;
;
(Ⅲ)定理:若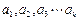 均为正数,则有
均为正数,则有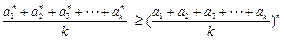 成立(其中
成立(其中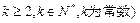 .请你构造一个函数
.请你构造一个函数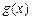 ,证明:
,证明:
当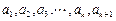 均为正数时,
均为正数时,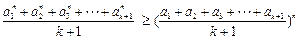 .
.
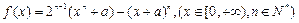 求函数
求函数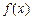 的最小值;
的最小值;(Ⅱ)证明:
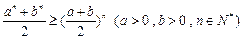 ;
;(Ⅲ)定理:若
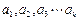 均为正数,则有
均为正数,则有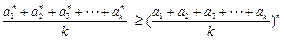 成立(其中
成立(其中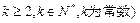 .请你构造一个函数
.请你构造一个函数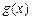 ,证明:
,证明:当
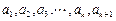 均为正数时,
均为正数时,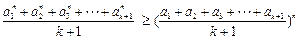 .
.(Ⅰ)当
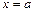 时,
时,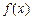 的最小值为
的最小值为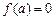 (Ⅱ)证明见解析(Ⅲ)证明见解析
(Ⅱ)证明见解析(Ⅲ)证明见解析(Ⅰ)令
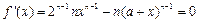
得
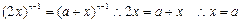 ……………………………………2分
……………………………………2分当
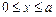 时,
时,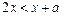
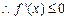 故
故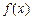 在
在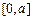 上递减.
上递减.当
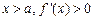 故
故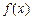 在
在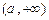 上递增.
上递增.所以,当
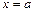 时,
时,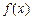 的最小值为
的最小值为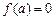 ….……………………………………..4分
….……………………………………..4分(Ⅱ)由
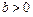 ,有
,有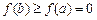 即
即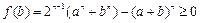
故
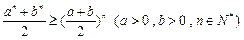 .………………………………………5分
.………………………………………5分(Ⅲ)证明:要证:
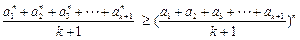
只要证:
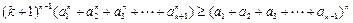
设
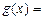
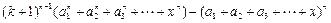 …………………7分
…………………7分则
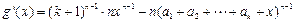
令
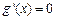 得
得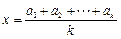 …………………………………………………….8分
…………………………………………………….8分当
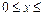
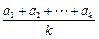 时,
时,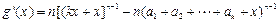
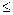

故
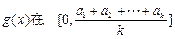 上递减,类似地可证
上递减,类似地可证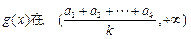 递增
递增所以
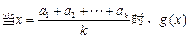 的最小值为
的最小值为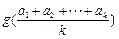 ………………10分
………………10分而
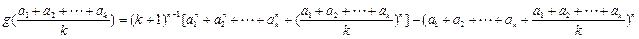 =
=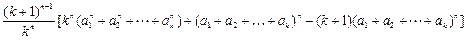
=
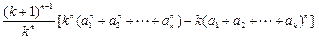
=
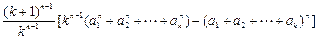
由定理知:
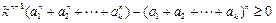 故
故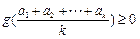
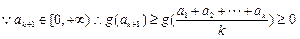
故
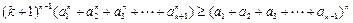
即:
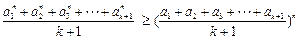 .…………………………..14分
.…………………………..14分………12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
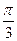 ,3)平移得到图象F′,若F′的一条对称轴是直线x=
,3)平移得到图象F′,若F′的一条对称轴是直线x=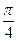 ,则θ的一个可能取值是
,则θ的一个可能取值是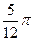
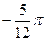

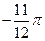
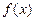 是定义在
是定义在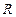 上的偶函数,当
上的偶函数,当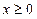 时,
时,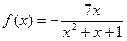 .
.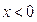 时
时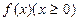 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;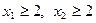 且
且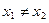 ,证明:
,证明: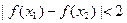 .
.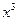 -ax在[1,+∞)上是单调函数.
-ax在[1,+∞)上是单调函数. ≥1,f(x)≥1,且f(f(
≥1,f(x)≥1,且f(f(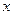 与人均消费
与人均消费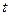 (元)的关系如下:
(元)的关系如下: 
 万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?
万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?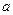
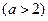 ,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。
,E、F、G、H分别是边AD、AB、BC、CD上的点,若AE=AF=CG=CH,问AE取何值时,四边形EFGH的面积最大?并求最大的面积。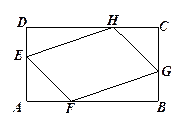
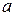 为实数,函数
为实数,函数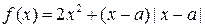 .
.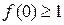 ,求
,求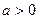 写出
写出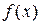 的单调递减区间;
的单调递减区间;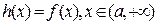
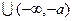 且
且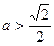 求不等式
求不等式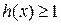 的解集.
的解集. 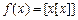 ,其中
,其中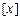 表示不超过x的最大整数,如:
表示不超过x的最大整数,如: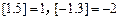 ,当
,当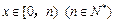 时,设函数
时,设函数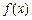 的值域为A,记集合A中的元素个数为an,则式子
的值域为A,记集合A中的元素个数为an,则式子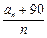 的最小值为( )
的最小值为( )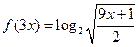 ,则
,则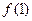 的值为( )
的值为( )