Question

【题目】已知函数f（x）＝lnx（b∈R），g（x）.

（1）讨论函数f（x）的单调性

（2）是否存在实数b使得函数y＝f（x）在x∈（，+∞）上的图象存在函数y＝g（x）的图象上方的点？若存在，请求出最小整数b的值，若不存在，请说明理由.（参考数据ln2＝0.6931，1.6487）

Answer 1

【答案】（1）答案不唯一，具体见解析（2）存在，最小b的整数值为2

【解析】

（1）求出函数的导数，分类讨论可得函数的单调性；

（2）假设存在实数使得函数在上的图象有在函数的图象上方的点，则使不等式成立，即成立，令，求新函数的最值即可判断.

（1）函数f（x）的定义域为（0，+∞），且f′（x），

当b≤0时、f′（x）＞0，函数f（x）在（0，+∞）上单调递增，

当b＞0时，若0＜x＜b，则f′（x）＜0，若x＞b，则f′（x）＞0，

函数f（x）在（0，b）上单调递减，在（b，+∞）上单调递增，

综上得：当b≤0时，函数f（x）在（0，+∞）上单调递增；

当b＞0时，函数f（x）在（0，b）上单调递减，在（b，+∞）上单调递增；

（2）假设存在实数b满足题意，则存在x∈（，+∞）

使不等式lnx成立，

即b＞ex﹣xlnx成立，

令h（x）＝ex﹣xlnx，则h′（x）＝ex﹣lnx﹣1，

令φ（x）＝ex﹣lnx﹣1，则φ′（x）＝ex，

因为φ′（x）在（，+∞）上单调递增、且φ′（）2＜0，φ′（1）＝e﹣1＞0，

且φ'（x）的图象在（，1）上连续，

所以存在x0∈（，1）使φ′（x0）＝0.即0，即x0＝﹣lnx0，

当x∈（，x0）时，φ（x）单调递减，当x∈（x0，+∞）时，φ（x）单调递增，

则φ（x）的最小值φ（x0）lnx0﹣1＝x01≥2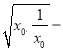1＝1＞0，

所以h'（x）＞0，h（x）在区间（，+∞）内单调递增，

所以h（x）＞h（）lnln2＝1.9952

所以存在实数b满足题意，且最小b的整数值为2.