题目内容
【题目】在平面直角坐标点xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=6.
(1)A为曲线C1上的动点,点M在线段OA上,且满足|OM||OA|=36,求点M的轨迹C2的直角坐标方程;
(2)点E的极坐标为(4,![]() ),点F在曲线C2上,求△OEF面积的最大值
),点F在曲线C2上,求△OEF面积的最大值
【答案】(1)x2+(y﹣3)2=9(y≠0)(2)![]()
【解析】
(1)直接利用转换关系式,把参数方程极坐标方程和直角坐标方程之间进行转换;
(2)利用三角形的面积公式的应用和三角函数关系式的恒等变换和正弦型函数的性质的应用求出结果.
(1)设点A(ρ1,θ),点M(ρ,θ),由于曲线C1的极坐标方程为ρsinθ=6,A为曲线C1上的动点,故![]() ,点M在线段OA上,且满足|OM||OA|=36,
,点M在线段OA上,且满足|OM||OA|=36,
所以![]() ,整理得点M的轨迹C2的直角坐标方程为x2+(y﹣3)2=9(y≠0).
,整理得点M的轨迹C2的直角坐标方程为x2+(y﹣3)2=9(y≠0).
(2)设F点为(ρ0,α),(![]() ),则ρ0=6sinα,|OF|=ρ0,且
),则ρ0=6sinα,|OF|=ρ0,且![]() (
(![]() ),或
),或![]() (
(![]() ),|OE|=4,
),|OE|=4,
所以![]() 12
12![]() 3
3![]() ,
,
由于![]() ,故当α
,故当α![]() 时,
时,![]() .
.

 阶梯计算系列答案
阶梯计算系列答案【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
或点赞.微信运动公众号为了解用户的一些情况,在微信运动用户中随机抽取了100名用户,统计了他们某一天的步数,数据整理如下:
|
|
|
|
|
|
|
| 5 | 20 | 50 | 15 | 5 | 5 |
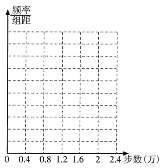
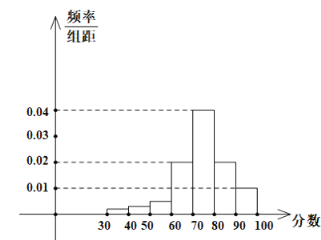
(1)根据表中数据,在如图所示的坐标平面中作出其频率分布直方图,并在纵轴上标明各小长方形的高;
(2)若视频率分布为概率分布,在微信运动用户中随机抽取3人,求至少2人步数多于1.2万步的概率;
(3)若视频率分布为概率分布,在微信运动用户中随机抽取2人,其中每日走路不超过0.8万步的有![]() 人,超过1.2万步的有
人,超过1.2万步的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.